さまざまなデータ構造（８）二分木１

2019-02-24データ構造

こんにちは。今回は木構造です。これまでに取り上げた連結リスト、スタック、キューはすべて１方向でした。それに対して、木構造は複数に分岐します。今回は高々２つの分岐までの木を扱います。このような木を二分木といいます。二分木を作るために、改めてノードから始めていきます。

1. 二分木のノード
2. 木についての用語
3. 木をつくろう！
4. 木を表示しよう！５つのたどり方

二分木のノード

連結リストでのノードは１方向だったので、次のノードにつながる矢印は１つでした。二分木では、２方向までの分岐が考えられるので、次につながる矢印を２つ作れるようにします。

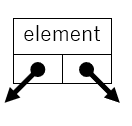
ここで、分岐が０または１のときは、矢印の代わりにnullにします。ノードの要素を表すelement、左右の部分木への矢印leftとrightをprivateのインスタンス変数として、これらへのアクセサを含めたクラスの定義は次になります。

package data_structure;

public class MyTreeNode<E> {

    private E element;
    private MyTreeNode<E> left, right;

    public MyTreeNode(E element, MyTreeNode<E> left, MyTreeNode<E> right) {
        this.element = element;
        this.left = left;
        this.right = right;
    }

    public E getElement() {
        return element;
    }

    public void setElement(E element) {
        this.element = element;
    }

    public MyTreeNode<E> getLeft() {
        return left;
    }

    public void setLeft(MyTreeNode<E> left) {
        this.left = left;
    }

    public MyTreeNode<E> getRight() {
        return right;
    }

    public void setRight(MyTreeNode<E> right) {
        this.right = right;
    }
}

木についての用語

木構造で最も上位にあるノードを根といいます。通常、木は地面に根をはっていますが、木構造を図示する際には、最上位のノードであることから、根を上にして書くことが多いようです。サムネイル画像の根を上にして表示すると次になります。

写真の上下をひっくり返して表現すると、とても違和感を感じますが、データ構造としての木構造の図ではほとんど違和感を感じないのは見慣れたせいでしょうか。次の図になります。

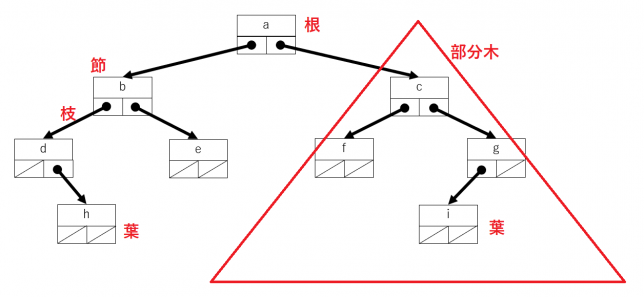
ノードは節ともいいます。節と節をつなぐ辺は枝といいます。先端にある節を葉といいます。完全に植物の木と同じ呼び方をしています。枝分かれした木の一部分だけ取り出しても、やはり木構造になっています。このような一部分を表す木を部分木といいます。二分木の場合、左右にそれぞれ部分木があるので、左右を区別するために左部分木と右部分木と呼ぶこともあります。

根に近い側の節（親）と枝の先にある節（子）を親子関係で表現したり、1つの親から出る左右の節を兄弟関係で表現したりすることもあります。データ構造を理解するためには、身近なものの比喩を使って表現されることが多くあります。データ構造やアルゴリズムの理解を深めるには、図を描いたり、知っているものに喩えたり、といった意外とプログラミングではない部分が大切なのではないかと思います。

木をつくろう！

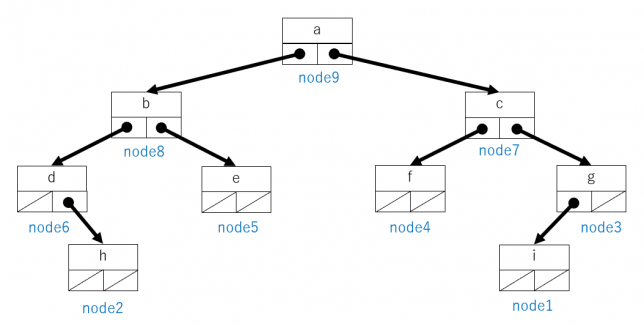
さしあたりノードを1つずつ作っていきます。先に葉の方から作っていきます。先に作ったノードを部分木として、後から根元に近いノードを作ります。１つずつノードを作っていくので、あまり見栄えがしないプログラムですが、後で要素を木に追加できるようなプログラムにします。とりあえずプログラムは次のようになります。

MyTreeNode<String> node1 = new MyTreeNode<String>("i", null, null);
MyTreeNode<String> node2 = new MyTreeNode<String>("h", null, null);
MyTreeNode<String> node3 = new MyTreeNode<String>("g", node1, null);
MyTreeNode<String> node4 = new MyTreeNode<String>("f", null, null);
MyTreeNode<String> node5 = new MyTreeNode<String>("e", null, null);
MyTreeNode<String> node6 = new MyTreeNode<String>("d", null, node2);
MyTreeNode<String> node7 = new MyTreeNode<String>("c", node4, node3);
MyTreeNode<String> node8 = new MyTreeNode<String>("b", node6, node5);
MyTreeNode<String> node9 = new MyTreeNode<String>("a", node8, node7);

図で表すと次のような木ができます。

木を表示しよう！５つのたどり方

木を根から順に系統立てて、すべての頂点をたどることを木の走査（traversal）といいます。走査する方法には５つの方法があります。

先行順(pre-order traversal)
中間順(in-order traversal)
後行順(post-order traversal)
深さ優先探索(breadth-first search)
幅優先探索(depth-first search)

これらについて説明します。

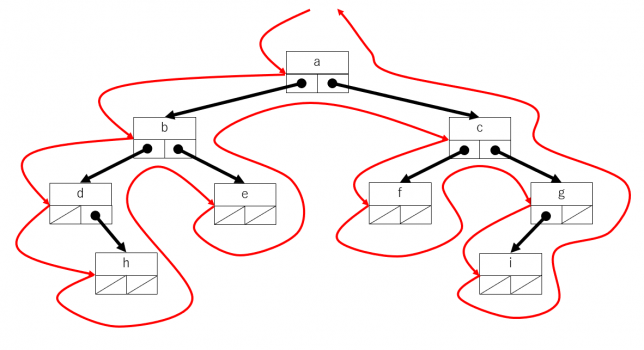
先行順走査(pre-order traversal)

頂点→左の部分木→右の部分木　という順序でたどっていきます。木を下図の表に表現した場合について説明します。根の左側から反時計回りにたどっていき、ノードの左側を通過するときにそのノードの要素を取り出すようにすれば先行順の走査になります。

簡単なプログラムは次になります。

String result = node.getElement();

if (node.getLeft() != null) {
	result += " " + preOrder(node.getLeft());
}

if (node.getRight() != null) {
	result += " " + preOrder(node.getRight());
}

中間順走査(in-order traversal)

左の部分木→頂点→右の部分木　という順序でたどっていきます。木を下図の表に表現した場合について説明します。根の左側から反時計回りにたどっていき、ノードの下側を通過するときにそのノードの要素を取り出すようにすれば中間順の走査になります。

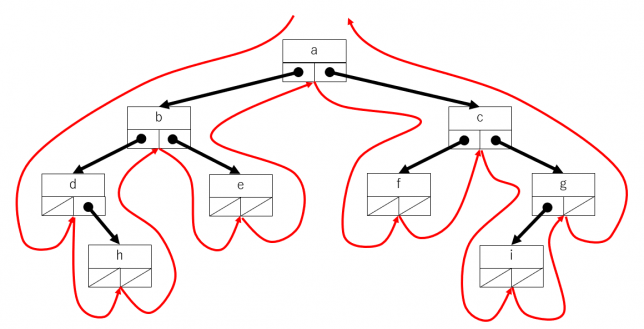
簡単なプログラムは次になります。

String result = "";

if (node.getLeft() != null) {
	result += inOrder(node.getLeft());
}

result += " " + node.getElement();

if (node.getRight() != null) {
	result += inOrder(node.getRight());
}

後行順走査(post-order traversal)

左の部分木→右の部分木→頂点　という順序でたどっていきます。木を下図の表に表現した場合について説明します。根の左側から反時計回りにたどっていき、ノードの右側を通過するときにそのノードの要素を取り出すようにすれば後行順の走査になります。

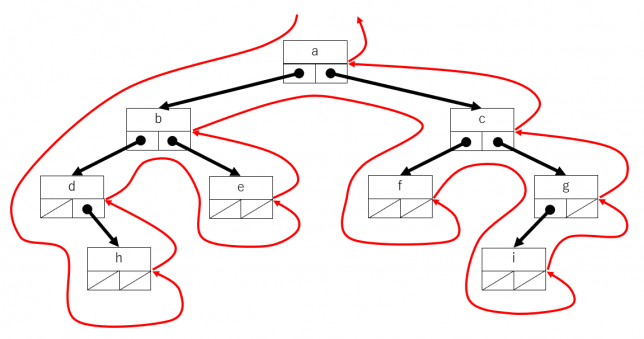
簡単なプログラムは次になります。

String result = "";

if (node.getLeft() != null) {
	result += postOrder(node.getLeft());
}

if (node.getRight() != null) {
	result += postOrder(node.getRight());
}

result += " " + node.getElement();

深さ優先探索(breadth-first search)

とにかく１方向に進めるだけ進んでいきます。今回は左側の枝があれば、どんどん左側に進むことにします。行き止まりになったら右側の部分木について左側に進めるだけ進みます。また行き止まりになったら右側の部分木があるところまで戻って・・・ということを繰り返します。

途中通過した右側の部分木をどのようにして残しておくかがポイントになりますが、以前取り上げたスタック（その１・その２）を使うと簡単にプログラムを書けます。

最初に根をスタックに積みます(push)。次にスタックから取り出して(pop)、右側の部分木・左側の部分木の順にスタックに積みます(push)。この順にしているのは、後から積んだものが先に取り出せるLIFOの特徴に合わせているためです。スタックが空になるまで繰り返せば、すべての頂点をたどることができます。

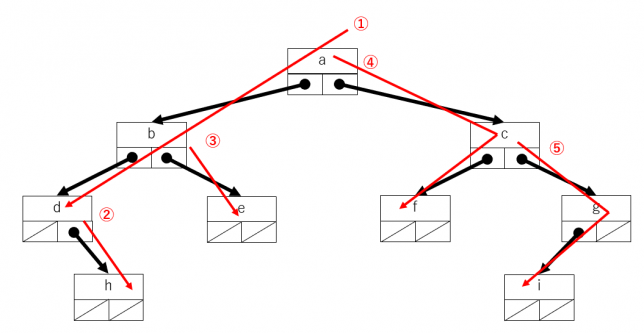
簡単なプログラムは次になります。

stack.push(node);

while (!stack.empty()) {
	tmp = stack.pop();
	result += " " + tmp.getElement();

	if (tmp.getRight() != null) {
		stack.push(tmp.getRight());
	}

	if (tmp.getLeft() != null) {
		stack.push(tmp.getLeft());
	}
}

幅優先探索(depth-first search)

幅優先探索は、木の根からの高さが同じものを順にたどります。すべて同じ高さをたどったら、１段階上の高さをたどります。これは以前取り上げたキュー（その１・その２）を使うと簡単にプログラムが描けます。

最初に根をキューに追加します(offer)。次にキューから取り出し(poll)、左側の部分木・右側の部分木の順にキューに追加します(offer)。キューを使うのは、先に追加されたものが先に取り出せるFIFOの特徴によるものです。キューが空になるまで繰り返せば、すべての頂点をたどることができます。

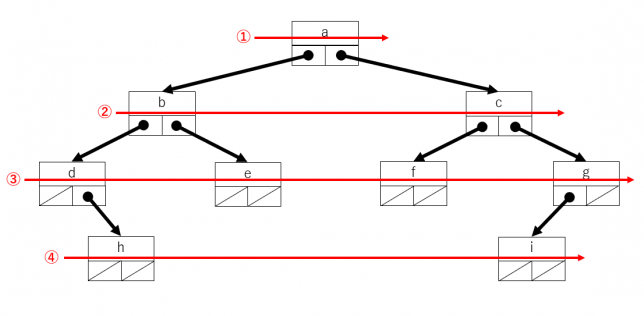
簡単なプログラムは次になります。

queue.offer(node);

while (!queue.isEmpty()) {
	tmp = queue.poll();
	result += " " + tmp.getElement();

	if (tmp.getLeft() != null) {
		queue.offer(tmp.getLeft());
	}

	if (tmp.getRight() != null) {
		queue.offer(tmp.getRight());
	}
}

次回、プログラムを整理したいと思います。今回はこれでおしまい。それではまた。

Posted by 春日井優