リサジュー図形

2018-09-30数学

こんにちは。前回、Ｐｙｔｈｏｎでのタートルグラフィックスを記事にしたので、せっかくなのでグラフィックス系の何かを書けないかと思いました。考えてみたところ、他教科の学習にも使える！ということで、タートルグラフィックスでリサジュー図形を描いてみることにしました。程よく描画速度が遅いので、実際に描いている様子を見ることができます。

リサジュー図形を学ぶのはどれくらいの人数？

リサジュー図形について学ばないで大人になっている人は多数います。リサジュー図形は「数学Ⅲ」の「平面上の曲線と複素数平面」で媒介変数による曲線として教科書に登場します。今の学習指導要領では、「数学Ⅲ」を履修しないと学校ではおそらく学びません。「数学Ⅲ」がどの程度学ばれているかというと、平成３０年度の教科書需要数は２５２０８５冊で、この冊数はおおむね受講生徒数と考えてよい人数です。おおよその１学年分の人数は、ほとんどの生徒が履修する「数学Ⅰ」「保健体育」「コミュニケーション英語Ⅰ」の需要数が参考になり約１２５万人です。大雑把ですが、５人に１人くらいの割合しか学習していないようです。

話は本題から外れますが、「社会と情報」の需要数は８６１７４１冊、「情報の科学」は１９２０５３冊です。

現状では、リサージュ図形を知っている人数とプログラミングを経験したことがある生徒では、リサジュー図形の人数の方に軍配が上がるようです。２０２２年には「情報Ⅰ」を履修してプログラミングを学ぶ人数と逆転しますが、それまではプログラミングの経験があるなら数学で使おう！という状況にはならないような気がします。それでも今回の記事を書いておきます。

リサジュー図形って？

ここまで、「リサジュー」図形と書いてきましたが、「リサージュ」図形と覚えている人は多いのではないでしょうか。物理学者のJules Antoine Lissajousさんが考案したことから名前がついています。この人の名前をフランス語の原語読みをすると「リサジュー」の方が近いということで、こちらの表記が増えてきているとのことです。

ｘ軸方向とｙ軸方向それぞれに単振動をさせて、それを合成させて軌跡が描く図形です。実際、どのような軌跡を描くかは、このページの終盤にタートルグラフィックスが描いたグラフを掲載しています。

単振動といってイメージが付かない人は振り子を想像してもらえばそれらしい感じです。縦方向と横方向に揺れるようにすれば、リサジュー図形が描けるようです。実際に描こうとして、振り子の先に粉が入った容器をぶら下げて少しずつこぼしながら描いている様子を掲載したサイトもあります。例えば

というような動画があります。

教科書で書かれる数式では、ｔを媒介変数として

\begin{cases}
x=\sin{mt}\\
y=\sin{nt}
\end{cases}

でｘ座標とｙ座標を計算できる図形です。コンピュータを使うのであれば、ｘ軸方向とｙ軸方向で振幅を変えたり、位相を変えたりすることもできます。

タートルグラフィックスでリサジュー図形を描いてみよう

早速ですが、Ｐｙｔｈｏｎのプログラムです。

import turtle
import math

kamepy = turtle.Turtle()

size = 200
m = 3
n = 4

x = size * math.sin( 0 )
y = size * math.sin( 0 )

kamepy.penup()
kamepy.goto( x , y )
kamepy.pendown()

for t in range(361):
    rad = math.radians( t )
    x = size * math.sin( m * rad )
    y = size * math.sin( n * rad )
    kamepy.goto( x , y )

１・2行目はタートルグラフィックスと数学関数のモジュールをインポートしています。４行目はタートルのオブジェクトを作成しています。前回の記事に続き、「亀ピ」という変数にしました。

６～８行目は、大きさとm、nの値を定義しています。

１０・１１行目は、ｔ＝０のときのｘ座標とｙ座標を求めています。１３～１５行目は、ペンを上げてタートルを初期位置に移動しています。

１７行目以降が描画部分です。１７行目のｆｏｒ文はｔの値を０～３６０までの繰り返しを作っています。ｔに０°～３６０°を代入することにしました。１８行目は度数法から弧度法に変換しています。数学の学習を兼ねるならば、ｒａｄｉａｎｓメソッドを使わないでπ／１８０°を掛けて求めた方がよいかもしれません。１９・２０行目はｘ座標とｙ座標をそれぞれ求めています。２１行目でタートルを移動して描画します。

リサジュー図形を描いてみた！（ｍ＝３，ｎ＝４のとき）

それでは、描画した画像を見てみましょう。

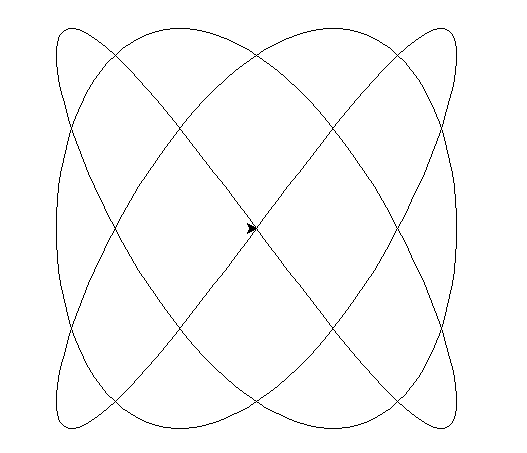
このページの画像だけ見ると、ふ～ん………という感じがします。ぜひ、プログラムを動かして徐々に描きあがっていく様子を見てください。

ｍ，ｎの値を変えて描画すると、いろいろ変化して楽しいですよ。

今回は以上でおしまい。それでは、また！