2019年の素数日(エラトステネスのふるい)

こんにちは。2018年最後の投稿になります。2018年を総括してもよいのですが、あまり気持ちが向いていません。
このサイトについての話では、年始にサーバへのインストールしていましたが、8月中旬まで放置していて約4か月だけの運用でした。
情報科については、学習指導要領が公示されたり、大学入試関係でも動きがあったりしました。1つ1つが未来に向かって進んでいるので、ちゃんと書いた方がいいように思っています。
そこで、2019年の話にします。といっても私が書く未来予測なんて与太話以上にはなりません。そこで、唐突ですが2019年の素数日について書くことにします。(書く時間が短そうという裏の理由もありますが・・・)
素数日とは
素数について復習しておきます。「1より大きい自然数で、約数が1とその自然数自身だけの数」です。平たく言うと「自然数で正の約数の個数が2個のもの」です。
次に素数日について判定します。例えばこの投稿の公開日2018年12月30日ですが、これを20181230としてその数が素数になっていれば素数日です。残念ながら20181230は、1でも自身でもない2を約数にもつため(2で割り切れるため)、素数日ではありません。
エラトステネスのふるい
素数判定法はいくつもありますが、かなり単純な「エラトステネスのふるい」を今回は使います。(プログラムのストックがあるから・・・)このアルゴリズムは比較的簡単で、for文の練習問題的な存在です。簡単に説明します。
Step1 チェック表を作る(1には素数でない目印をつける)
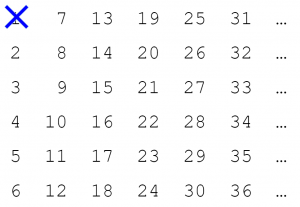
Step2 チェックされていない最小の数は素数で、その倍数に素数でない印をつける
Step3 チェックされていない最小の数を2乗して、最大数を超えるまで、Step2を繰り返す
(Step2-1 チェックされていない最小の数2は素数で、2の倍数に×をつける)
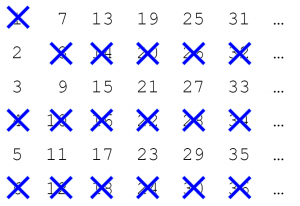
(Step2-2 チェックされていない最小の数3は素数で、3の倍数に×をつける)
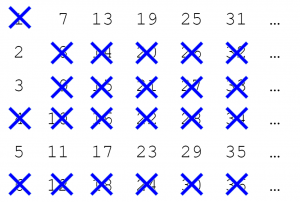
(Step2-3 チェックされていない最小の数5は素数で、5の倍数に×をつける)

(Step3-3 次のチェックされていない最小の数7を2乗すると、最大数36を超えるので、以上で繰り返しは終了)
Step4 この時点で×がついていない数が素数
エラトステネスのふるいでの工夫
繰り返しの終了条件
上のStep3で、「チェックされていない最小の数を2乗して、最大数を超えるまで」繰り返しています。×が付いていない数は、上の表では7~31まで8個も残っています。その理由を確認します。
素数でない数として36を例に考えてみます。36を2つの数の積で表すと
1×36、2×18、3×12、4×9、6×6、9×4、12×3、18×2、36×1
があります。これより6×6の前後で対称になっていることがわかります。チェックされていない最小の数を2乗して最大数を超えたら、新たに×が付くことはないため、計算時間がかかるだけで無駄な計算です。
素数になりうる数
偶数は2の倍数です。自然数で最初の偶数である2は素数ですが、それ以外の偶数は素数でないことはすぐにわかります。また、偶数は他の数の倍数よりも圧倒的に多いため、チェックするにも時間がかかります。偶数のチェックをしなければ時間短縮につながります。
さらに3の倍数も数が多いので工夫してみましょう。2と3の最小公倍数である6の倍数に着目して表を再確認してみます。

6で割ったときに、余りが0・2・4のものは偶数です。また、余りが0・3のものは3の倍数です。これらは素数ではありません。そうすると、素数になりうる候補は、6で割ったときの余りが1・5のいずれかに限られます。これを用いると、さらに時間短縮できます。
エラトステネスのふるいのプログラム
今回はJavaのプログラムを掲載します。出力は2019年の素数日だけが表示されるようにしています。なお、上で素数になりうる数は6で割って余りが1・5だけと書いていますが、紹介するプログラムでは偶数だけを除外したものになっています。
package prime_number;
public class PrimeNumber {
public static void main(String[] args) {
int N = 20191232;
boolean[] prime = new boolean[N + 1];
for (int i = 1; i <= N; i++) {
prime[i] = true;
}
prime[1] = false;
for (int i = 3; i <= Math.sqrt(N); i+=2) {
if (!prime[i])
continue;
for (int j = 3; i * j <= N; j+=2) {
prime[i * j] = false;
}
}
int count=1;
int[] days = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
for (int m = 1; m <= 12; m++) {
for(int d = 1; d<=days[m-1]; d+=2) {
int i = 20190000 + m*100 + d;
if (prime[i]) {
System.out.println(i);
count++;
}
}
}
System.out.println(count);
}
}
この出力は次の通りです。
20190221
20190227
20190301
20190319
20190323
20190421
20190523
20190529
20190601
20190613
20190719
20190811
20190823
20190913
20191009
20191027
20191109
20191117
20191231
20
2019年の最初の素数日は2月21日で、大晦日も素数日、年間通して20日あります。ちなみに2018年最後の素数日は2018年12月29日で、この記事の公開前日でした。
さらについでの話ですが、今上天皇が天皇としての最後の誕生日2018年12月23日、皇太子殿下が天皇に即位して最初に迎える誕生日2020年2月23日の両方とも素数日です。
素数にまつわるアルゴリズムはたくさんあるので、そのうちきっと取り上げると思います。それでは、よいお年をお迎えください。
[mathjax]












ディスカッション
コメント一覧
まだ、コメントがありません