似ている?似ていない?いろいろな距離

こんにちは。データサイエンスの話に入っていく前に、似ているか似ていないかを判定するために、距離について整理しておきたいと思います。距離というと、2点間を線分で結んだときの長さを考えるかもしれません。そればかりではないことを確かめていきましょう。
ユークリッド距離
私たちが一番馴染みがある距離がユークリッド距離です。平面(2次元)で距離を求めるには、三平方の定理を考えれば求められます。
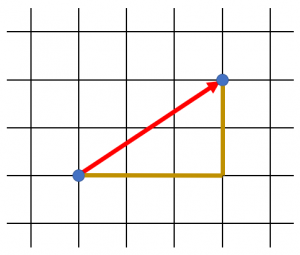
空間図形(3次元)についても、数学ではどのように求めるかといった問題が出てきます。図形的な意味を離れて、高次元になっても拡張して考えることができます。
数式ですが、2次元では\( d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}\)、3次元では\( d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}\)になります。さらに次数が増えた場合には同様に拡張できます。
マンハッタン距離
日本で同じような距離を名付けていたら、「京都距離」とか「札幌距離」という名前になったかもしれません。京都ならば烏丸塩小路(京都駅の烏丸口を出たあたり)から寺町御池(本能寺のあたり)までの距離は?であるとか、札幌ならば北1西2(時計台)から南4西3(すすきののニッカ看板)までの距離は?ということを考えたときに、建物をぶち抜いていくことはできず、通りに沿って行くしかありません。このような格子状の道路を通っていく距離がマンハッタン距離です。
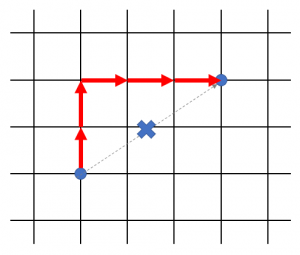
数式ですが、2次元では\( d= | x_{2}-x_{1} | + | y_{2}-y_{1} | \)、3次元では\( d= | x_{2}-x_{1} | + | y_{2}-y_{1} |+ | z_{2}-z_{1} | \)になります。さらに次数が増えた場合には同様に拡張できます。
京都は通りに名前が付いていて、囲碁の碁盤のような感じです。札幌は区画に番号が付いていて、将棋盤のような感じです。そうすると、「京都距離」とか「平安京距離」なのかな・・・?
チェビシェフ距離
将棋で、王将(玉将)は自分のいるマスの8方向に一つだけ進めます。王将が1手で進める場所はすべて「チェビシェフ距離=1」、王将が2手でなければいけない場所はすべて「チェビシェフ距離=2」となります。
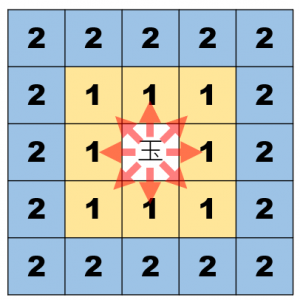
数式で求めると、2次元では\(d=max(|x_{2}-x_{1}|,|y_{2}-y_{1}|)\)、3次元では\(d=max(|x_{2}-x_{1}|,|y_{2}-y_{1}|,|z_{2}-z_{1}|)\)になります。さらに次元が増えた場合には同様に拡張できます。
誰も考えていないと思いますが、餃子の王将までの距離ではありません。ここでの餃子の王将が、京都王将なのか、大阪王将なのかは聞かないでください。
レーベンシュタイン距離
突然ですが、福島県と福岡県と福井県ってひらがなで書いても似ていますよね!「ふくしまけん」「ふくおかけん」「ふくいけん」絶対に似ている!
これを1文字挿入、1文字削除、1文字置換の3つの操作を何回行えば変換できるかがレーベンシュタイン距離になります。
| ふ | く | し | ま | け | ん |
| ↓ | |||||
| ふ | く | お | ま | け | ん |
| ↓ | |||||
| ふ | く | お | か | け | ん |
ということで、2回の置換で変換できたので、「ふくしまけん」と「ふくおかけん」では「レーベンシュタイン距離=2」です。
| ふ | く | し | ま | け | ん |
| ↓ | |||||
| ふ | く | い | ま | け | ん |
| × | |||||
| ふ | く | い | け | ん |
ということで、1回の置換と1回の削除で変換できたので、「ふくしまけん」と「ふくいけん」では「レーベンシュタイン距離=2」です。
「ぐんま」と「とちぎ」ではどちらが「とうきょう」に近いのでしょうか?
| ぐ | ん | ま | と | ち | ぎ | |||||
| ↓ | ↓ | |||||||||
| と | ん | ま | と | う | ぎ | |||||
| ↓ | ↓ | |||||||||
| と | う | ま | と | う | き | |||||
| ↓ | ○ | |||||||||
| と | う | き | と | う | き | ょ | ||||
| ○ | ○ | |||||||||
| と | う | き | ょ | と | う | き | ょ | う | ||
| ○ | ||||||||||
| と | う | き | ょ | う |
ということで、ぐんまとのレーベンシュタイン距離=5、とちぎとのレーベンシュタイン距離=4ということで、「とちぎ」の方が「とうきょう」に近いようです。「いばらき」はどうなんでしょうか?別に北関東の争いに油を注ぐつもりはありません。
ちなみに2018年度の慶応義塾大学の入試問題で出題されていました。(情報ーV)
ジャッカード係数・ジャッカード距離
2つの文章で、同じ言葉が出てくると似た文章のような気がします。あまり同じ言葉が出なければ無関係そうです。
Twitterのフォロワーのメンバーが似ていると、同じ学校・同じクラス・同じ部活のような共通点が多そうに感じますよね。フォロワーのメンバーが重なっていないと、本人どうしも親しくなさそうな感じがします。本人どうしが似ていれば、共通しないフォロワーを、「おすすめのアカウント」として紹介できますね。
Amazonで同じものをよく買う2人は、趣向が似ているように思えます。違うものを買う2人は、買い物の傾向が違うのでしょう。このような判定ができれば、趣向が似ている人に対して、片方の人だけが購入しているものをもう一方の人に勧めると買ってくれるかもしれません。このような時に使う値がジャッカード係数です。2つのものの類似度を表しています。逆に離れている程度ということを数値化したジャッカード距離というものもあります。
数式では、ジャッカード係数は\(\displaystyle \frac{\vert A \cap B \vert}{\vert A \cup B \vert}\)、ジャッカード距離は\(\displaystyle \frac{\vert A \cup B \vert – \vert A \cap B \vert}{\vert A \cup B \vert}\)になります。
例として、ここではジャッカード係数を求めます。
佐藤={高橋,田中,伊藤,渡辺}
鈴木={高橋,田中,伊藤,山本}
中村={高橋,田中,伊藤,小林,加藤}
吉田={高橋,山田,佐々木,山口}
というフォロワーがいるとします。
佐藤さんと鈴木さんのジャッカード係数を求めます。\(佐藤 \cap 鈴木=\{高橋,田中,伊藤\} \),\(佐藤 \cup 鈴木=\{高橋,田中,伊藤,渡辺,山本\} \)となるので、\( \frac{3}{5}\)です。
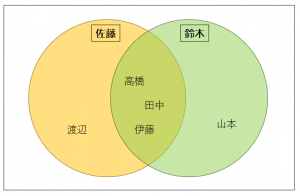
佐藤さんと中村さんのジャッカード係数を求めます。\(佐藤 \cap 中村=\{高橋,田中,伊藤\} \),\(佐藤 \cup 中村=\{高橋,田中,伊藤,渡辺,小林,加藤\} \)となるので、\( \frac{3}{6}\)です。
佐藤さんと吉田さんのジャッカード係数を求めます。\(佐藤 \cap 吉田=\{高橋\} \),\(佐藤 \cup 吉田=\{高橋,田中,伊藤,渡辺,山田,佐々木,山口\} \)となるので、\( \frac{1}{7}\)です。
ということで、佐藤さんのジャッカード係数の近さは、中村さん・吉田さんより鈴木さんの方が近いことになります。共通していないフォロワーは、もしかしたらつながりがある人じゃないか?と予想できます。
Amazonで「他の人はこのようなものを買っています」とか、SNSで「おすすめのユーザ」とか表示されることがありますが、余計なお世話と言いたいです。
ハミング距離
2つの等しいビット数(文字数)のものを比較するとき、対応するビット(文字)で異なっているものの個数がハミング距離です。情報通信でノイズが入ってビットの判定がおかしくなることはあるでしょう。例えば
送信 : 11011010
受信 : 10111100
と4か所異なっているので、ハミング距離=4です。こんなに誤りがある通信システムならば、早急に更新してほしいものです。
コサイン類似度
高校の数学でベクトルで内積という計算をしました。ベクトルの掛け算を考えようとしたときに、多変量(高校数学ではx,y平面の座標)の値でどのように積を考えるかが問題になります。図形的には、2つのベクトルのうち、片方をもう片方に正射影して(垂直に写し取って)、同一直線上に揃えて大きさを掛けます。これを内積といいます。そうすると数式では、
\[ \vec{a} \cdot \vec{b} = |\vec{a}| \times \cos \theta \times |\vec{b}| \]
と表せます。次の図のように\(\vec{a}\)を\(\vec{b}\)に写し取って、同一直線上にして大きさをかけています。
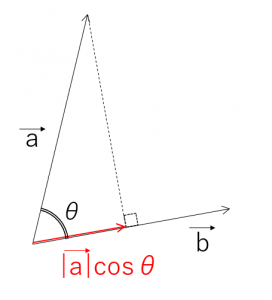
ここで、(正確さはありませんが)似ているということを「向きが同じ」かどうかで判定することにしましょう。向きとは2本のベクトルのなす角のことです。そこで、\( \cos \theta \)を求めると
\[ \displaystyle{ \cos \theta = \frac{ \vec{a} \cdot \vec{b} }{\vert \vec{a}\vert \vert \vec{b} \vert} } \]
となります。2本のベクトルのなす角が0°に近ければ同じ方向を向いているので「似ている」、2本のベクトルがなす角が90°に近ければ「関係ない」とするのが、コサイン類似度です。
その他の距離や類似度
距離や類似度について書き始めて、この世界が恐ろしいことがわかりました。調べれば調べるほど、さまざまな距離や類似度が見つかってしまいます。
- ジャロ・ウインクラー距離
- マハラノビス距離
- ダイス係数
- シンプソン係数
- ピアソンの相関係数
どこまで取り上げようか迷いましたが、力尽きました・・・
距離の公理
ここで距離についての議論の出発点となる公理を確認しておきます。
実数値関数\(d(x,y)\)が次を満たすとき、\(d(x,y)\)を距離といいます。
1)\(d(x,y) \geq 0\)(非負性)
2)\(x=y \Leftrightarrow d(x,y)=0\)(非退化性)
3)\(d(x,y)=d(y,x)\)(対称性)
4)\(d(x,z) \leq d(x,y) + d(y,z) \)(三角不等式)
これらは、距離についての議論の出発点です。
距離で注意すること
昔、結婚する相手の条件で「三高」がもてはやされた時期がありました。別に日大三高とか、農大三高とか、古河三高とか、仙台三高のことではありません。
「高学歴・高身長・高収入」が結婚の条件といわれていたようです。そんなふざけた奴は、ジジババになったとき「高血圧」「高血糖」「高尿酸値」の三高になってしまえ!と思ってしまうのは、自分自身が三高のどれ一つ満たしていないからでしょうか。
本題に戻りますが、(偏差値,身長,月収)という3次元のベクトルがあったとしましょう。平均値は偏差値は50です。総務省の2017年の統計で、高校3年生の平均身長は170.7cm、での月収の平均値は約31万円だそうです。次の3人のうち、一番平均からの距離が大きいのは誰でしょう。1人目高偏差値で(75,171,31万),2人目高身長(50,195,311万),3人目高収入(50,171,1000万)この3人では、平均値(50,170.7,31万)とのユークリッド距離を求めると、計算するまでもなく3人目の高収入の人が距離が大きいことになります。結局カネが重要なんですよ。
という比較が問題になるのは、3つの値の尺度が大幅に違うためです。今回の例では「高学歴・高身長・高収入」の中で数値として特に収入が開きが大きいです。
と自分とは無縁の話を書いていたら、嫌気がさしてきたので、おしまいにします。それではまた。









ディスカッション
コメント一覧
まだ、コメントがありません