さまざまなデータ構造(10)二分探索木1

こんにちは。今日は3の倍数の日ではありませんが、2月の更新が9回になってしまうので更新することにします。
前々回・前回の2回で二分木について取り上げました。さらに発展して今回は二分探索木を取り上げたいと思います。
前置き
このサイトのタイトルが「情報科 いっぽ まえへ!」で、本当ならば高校の授業を前に進めようという趣旨で、高校の先生か高校生あたりが読者のターゲットと考えています。それにしては、内容が高度すぎるのではないかと思われる方もいるかもしれません。情報Ⅰ・情報Ⅱのいずれでも高度なデータ構造を扱う場面はなさそうです。専門科目では「情報システムのプログラミング」に木構造がかろうじて現れる程度です。
しかし、世の中には高校生までを対象にした情報オリンピックなんてものもあり、多少複雑なデータ構造やアルゴリズムを扱ってもよいかなと思いながら書いています。実際は、情報オリンピックなどの競技プログラミングをやる人は、自分でこのようなデータ構造を実装しないでライブラリを使うと思います。しかし、データ構造がどうなっているかについてや、その実装方法のアイデアなどを知っておくと応用が利くかなと思います。競技プログラミングを意識しているのに、なぜJavaなのかというと、私にとって限られた時間で一番早く書けるからです。本当ならばCかC++で書かなければダメですよね・・・すみません。どこかのタイミングでC++のバージョンを書こうと思いますが、多分ネット上を探せば見つかると思いますので、他のサイトを当たってください。
もしかしたら大学生が苦しまぎれに検索していたら、このサイトにたどり着くのかもしれません。情報系の学科の学生さんは、これくらいのコードは自力で書けて当然という力を求められますので、写経やコピペに使わないで、参考程度に見てもらいたいと思っています。
二分探索木とは
それでは、ようやく本題に入りたいと思います。
前回まで二分木を取り上げました。ざっくりまとめると、枝の本数が高々2本までの木でした。この二分木に、さらに条件を付けます。あるノード(☆)のelementと比較して、☆ノードの左部分木に含まれるノードのすべてのelementは☆ノードのelementより小さい値であり、☆ノードの右部分木に含まれるノードのすべてのelementは☆ノードのelementより大きい値である二分木を二分探索木といいます。
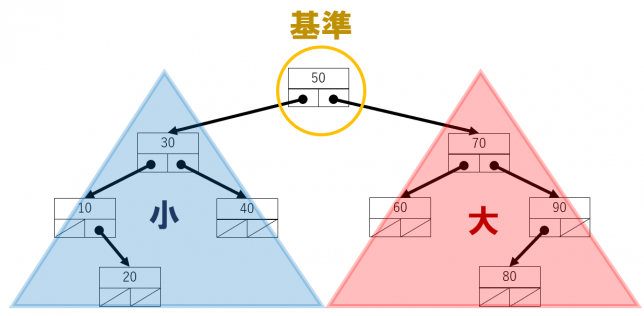
二分探索木は中間順に走査すると昇順に整列します。二分探索木でデータを挿入したり削除したりする際に、この関係性が崩れないようにする必要があります。これが意外と面倒です。特にデータを削除する場合、どこのデータがなくなるかがわからないのでますます面倒です。
二分探索木での探索
二分探索木という名前だけあって探索にはとても強いです。左右の部分木で、データが概ね半々に分かれるので探索する回数は\(O(\log n)\)になります。\(O\)表記法はここでは深入りしませんが、データの個数を\(n\)個としたとき計算量や計算時間がどの程度になるかを見積もる表記法と考えておけば、大外れはしないと思います。ここで、\(O(\log n)\)がどの程度かというと、データの個数が2倍になっても+1、データの個数が4倍になっても+2、データの個数が1024倍になっても+10程度しか増えないという増え方になり、とても効率がよいものです。ただし、これは左右のバランスがよい場合で、片方に寄ってしまった場合には、単なる線形探索になってしまうので\(O(n)\)になります。
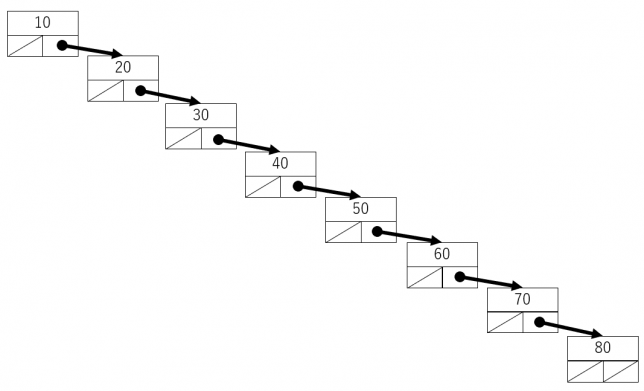
探索のアルゴリズムは、部分木の大小関係を使いながら枝を順にたどっていくというものです。葉にたどり着いていなく探す値が見つからない間、先の枝に進むいうことになります。図示すると次になります。
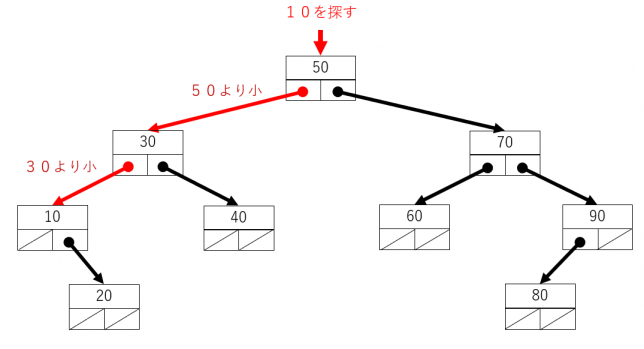
見つからない場合は次になります。
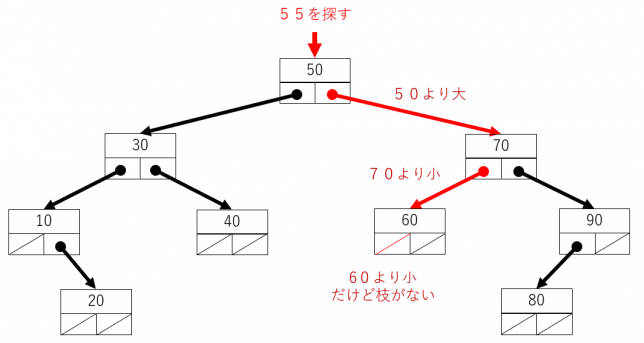
これをJavaで書くと次のようになります。
public MyTreeNode<Integer> find(Integer element) {
MyTreeNode<Integer> node = root;
while (node != null && node.getElement() != element) {
if (element < node.getElement()) {
node = node.getLeft();
} else {
node = node.getRight();
}
}
return node;
}
二分探索木への挿入
大きく分けて、ノードがない空っぽの木の根に挿入する場合と、それ以外に分けて考えます。
空っぽの木の場合には、挿入するデータを根にします。
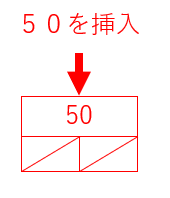
それ以外の場合は、部分木の大小を考えて左右のいずれかの枝に進みます。進みたい側の枝がなければ、そこに新しいノードを追加します。
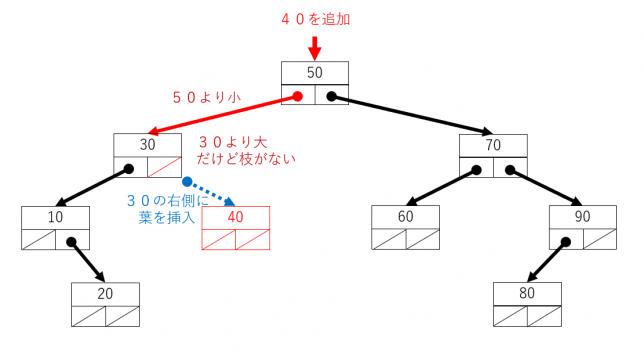
これをJavaで書くと次のようになります。
public void insert(Integer element) {
if (root == null) {
MyTreeNode<Integer> tmp = new MyTreeNode<Integer>(element, null, null);
root = tmp;
return;
}
insert(root, element);
}
private void insert(MyTreeNode<Integer> node, Integer element) {
if (element < node.getElement()) {
if (node.getLeft() == null) {
MyTreeNode<Integer> tmp = new MyTreeNode<Integer>(element, null, null);
node.setLeft(tmp);
return;
} else {
insert(node.getLeft(), element);
return;
}
} else {
if (node.getRight() == null) {
MyTreeNode<Integer> tmp = new MyTreeNode<Integer>(element, null, null);
node.setRight(tmp);
return;
} else {
insert(node.getRight(), element);
return;
}
}
}
再帰を使って書いていますが、たどっていくためのノードを変数として用意すれば再帰でなくても書けると思います。
さて、残りはデータの削除になりますが、枝の本数によって場合分けが必要になるため長くなりそうです。ということで、中途半端な感じはしますが今回はこれでおしまいにします。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません