さまざまなデータ構造(11)二分探索木2

こんにちは。前回は二分探索木とは何かについて説明し、探索と挿入について書きました。前回やり残したデータの削除について書きます。
データの削除
二分探索木でデータを削除するには工夫が必要です。この記事を書くために他のサイトも確認したのですが、データの削除の方法は書かれていてもプログラムを実装していないサイトも少なからずありました。やはり面倒なようです。私が書いたコードを載せますが、きれいに書けませんでした。もう少し精進します。
面倒な理由は、単純にノードを削除できる場合と、ノードのつなぎ変えが必要になる場合があるためです。ここでは、
- データが存在しない場合
- 削除するデータに子ノードがいない(葉)である場合
- 削除するデータに子ノードが1つだけの場合
- 削除するデータに子ノードが2つある場合
に分けて説明します。
データが存在しない場合
データが存在しない場合は削除するノードがないので、削除できなかったという意味でfalseを戻り値として終了します。
Javaのプログラムは次になります。
if (find(element) == null) {
return false;
}
削除するデータを見つける
削除するデータを見つけます。一つ上の世代のノードを使わないとつなぎ変えができないので、parentとchildの2つの世代のノードを記憶しながらたどっていきます。たどり方は探索の時と同じで、elementと比較しながら左右を決定します。
Javaのプログラムは次になります。
MyTreeNode<Integer> parent = null;
MyTreeNode<Integer> child = root;
while (child.getElement() != element) {
if (element < child.getElement()) {
parent = child;
child = child.getLeft();
} else {
parent = child;
child = child.getRight();
}
}
削除するデータが見つかった時点では、削除するノードはchildのノードになります。その親であるparentのsetLeftまたはsetRightのメソッドを使う必要があるので、parentも変数として用意しています。
削除するデータに子ノードがいない(葉)である場合
削除するデータが葉である場合には、単にそのノードにつながる枝を切ってしまえばおしまいです。枝を切るというのは、葉につながっていた枝の替わりにnullを代入すればよいことになります。
削除する葉が根でもある場合、root=nullとします。これにより削除できることは、根も葉もない事実です。
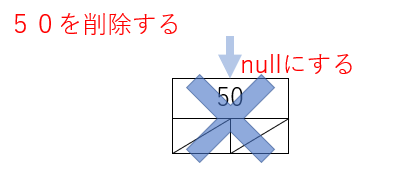
Javaのプログラムは次になります。データを削除できたので、trueを戻り値として終了します。
if (child == root) {
root = null;
return true;
}
削除するノードが左側の枝の場合、parentの左側にnullを代入することで、データを削除できます。
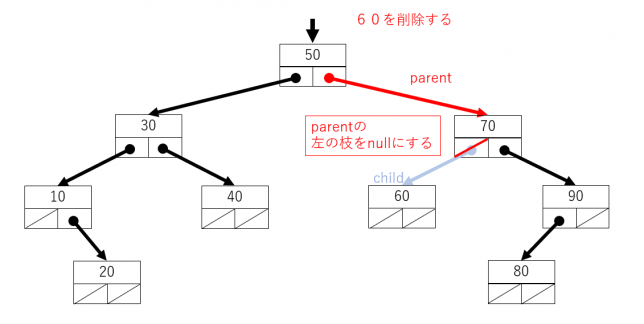
同様に、削除するノードが右側の枝の場合、parentの右側にnullを代入することで、データを削除できます。
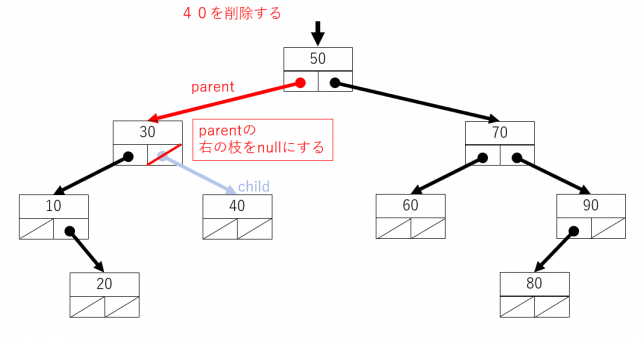
Javaのプログラムは次になります。データを削除できたので、trueを戻り値として終了します。
if (child == parent.getLeft()) {
parent.setLeft(null);
} else {
parent.setRight(null);
}
return true;
削除するデータに子ノードが1つだけの場合
1つだけある子ノードをnodeという変数で記憶しておきます。
MyTreeNode<Integer> node;
if (child.getLeft() == null) {
node = child.getRight();
} else {
node = child.getLeft();
}
削除するデータが根の場合、先ほど記憶しておいたnodeにrootを替えます。
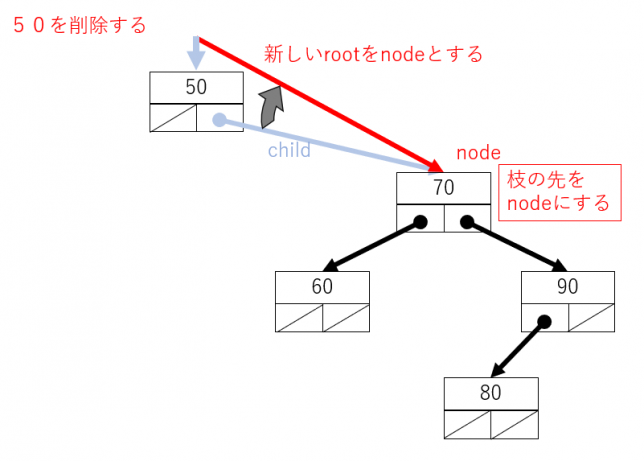
削除する節がparentの左側につながっている場合には、左側の枝を先ほど記憶しておいたnodeに替えます。
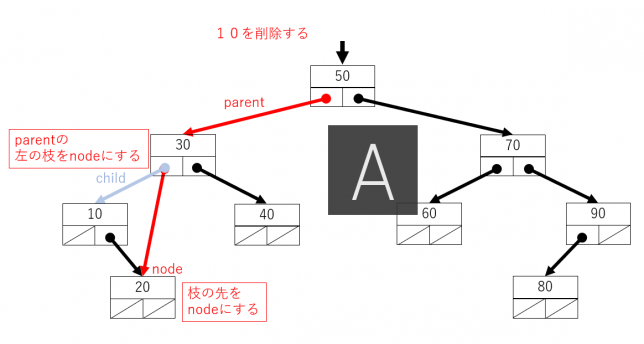
同様に、削除する節がparentの右側につながっている場合には、右側の枝を先ほど記憶しておいたnodeに替えます。
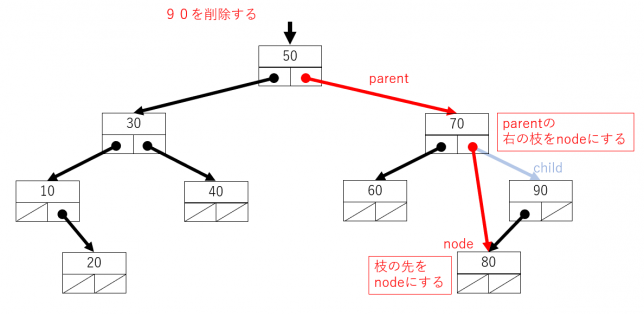
Javaのプログラムは次になります。データを削除できたので、trueを戻り値として終了します。
if (child == root) {
root = node;
} else if (child == parent.getLeft()) {
parent.setLeft(node);
} else {
parent.setRight(node);
}
return true;
削除するデータに子ノードが2個ある場合
この記事を書くにあたり、子ノードを2個ある場合には、左部分木の最大のノード(または右部分木の最小のノード)を削除するノードの替わりにするというアルゴリズムが書かれているものが多くありました。
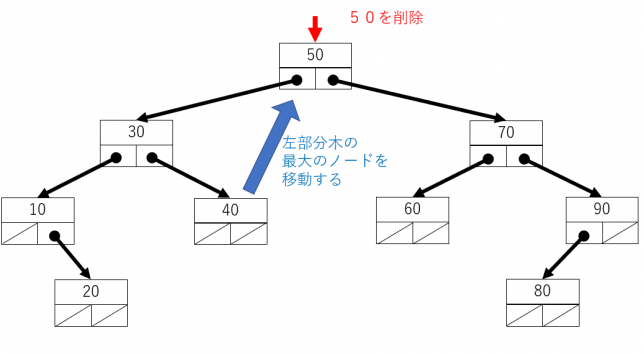
確かにこれでノードを削除できますが、私自身が考えたのは、削除するノードの右部分木を、左部分木の最も右に接ぎ木するというものです。(左右を逆にしても大丈夫です)こちらのアルゴリズムが採用されないのは、削除後の木の高さを比較すると、高い位置にあるノードに接ぎ木するため、どうしても木が高くなってしまうためだと思います。そのような欠点があることを承知の上で、自分が考えたアルゴリズムを実装します。(ノードを移動する削除方法は、別のサイトに載っているのでそちらをご覧ください)
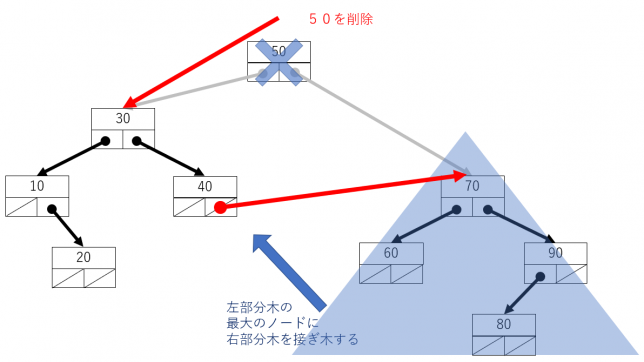
Javaのプログラムは次になります。データを削除できたので、trueを戻り値として終了します。
if (child == root) {
root = child.getLeft();
} else if (parent.getLeft() == child) {
parent.setLeft(child.getLeft());
} else {
parent.setRight(child.getLeft());
}
MyTreeNode<Integer> node = child.getRight();
child = child.getLeft();
while (child.getRight() != null) {
child = child.getRight();
}
child.setRight(node);
return true;
プログラムの前半は根に近い方に残す処理をして、後半は接ぎ木する先を見つけてつなぐ処理をしています。
本当はよりよいアルゴリズムを選択していく姿勢が大切なのかもしれませんが、何かを見て単に覚えるだけではなく、自分なりに考えることも大切だと思い、あえて効率面で劣るアルゴリズムを載せることにしました。
これで二分探索木からデータを削除できるようになりました。プログラムが多めですが、約2900文字と図が8枚ということで、今回はこれでおしまいにします。次回は二分探索木のプログラムをまとめます。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません