写像

こんにちは。今回は突然ですが写像について取り上げたいと思います。
写像を取り上げた理由
昔の高校の数学では写像が学習内容に含まれていましたが、平成元年公示の学習指導要領以降は消えてしまいました。しかし、簡単に概念だけでもよいので知っていた方がいいような気がします。例えば、機械学習で画像認識をする場合には、画像から対象物の名称に、画像から人物名に、といった対応が付けられます。パスワードの暗号化などでは、平文から暗号化された文字列への対応になっています。文字から文字コードへの対応付け、その逆の文字コードから文字への対応付けといった双方向の対応付けがあります。
残念ながらこのような対応付けは、今の数学では数値から数値への対応付けがなされている関数だけしか扱われていません。(写像にあたらない関数もありますが・・・)このような対応付けは至るところにあります。それらを抽象化した概念である写像について知ることにより、対応付けであったり、変換であったりについて、集合の考えとあわせて意識できるように思います。ということで、写像を取り上げることにしました。
写像とは
\(A\),\(B\)を集合とするとき、集合\(A\)のそれぞれの元に対して、集合\(B\)のうちただ1つの元を対応付ける規則のことを\(A\)から\(B\)への写像といいます。記号を使い、\(f\)が集合\(A\)から集合\(B\)への写像であることを\(f:A\rightarrow B\)と表します。集合の元を用いると、\(f:a\mapsto b\)であるとか\(b=f(a)\)と表します。
吉野家で
\(A=\{小盛,並盛,アタマの大盛,大盛,特盛,超特盛\}\)
という牛丼のサイズの集合に対して
\(B=\{1円,2円,3円,\cdots\}\)
という税込価格の集合への対応は基本的にただ1つだけ決まります。(割引券や白犬の金曜日のような場合については差し当たり考えないものとします)これは、牛丼のサイズから税込価格という写像になります。必ずしも数値の集合でなくても構わないところが、関数よりも広い概念になります。
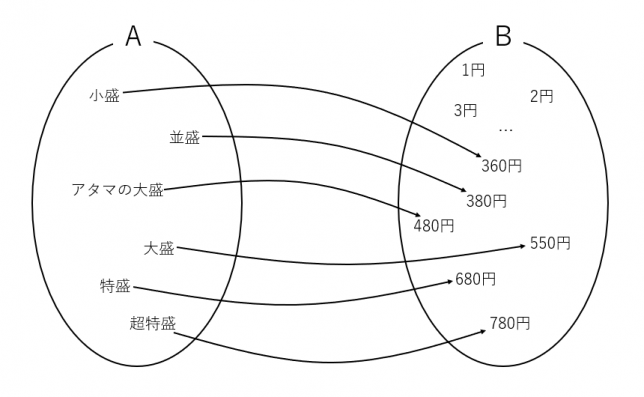
吉野家のサイトをよ~く見ていると、ショッピングモールやサービスエリアなど一部店舗では税込価格が異なっていることが書かれています。それ踏まえて図にすると次のようになります。
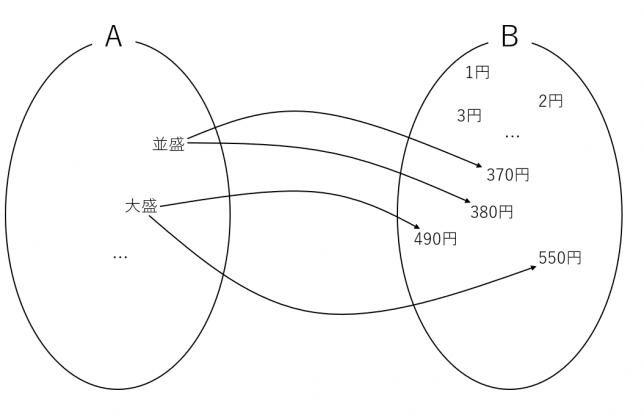
この場合には、集合\(A\)から集合\(B\)に対してただ1つの元が決まらないので写像ではありません。以降、写像を考えるために価格が異なる店舗を含めずに考えていくことにします。
集合の直積に対する写像
先ほどの吉野家の例では、集合\(A\)の値から集合\(B\)の値への対応という写像を考えました。必ずしも1つの集合から別の集合への対応に限られる必要はありません。
例えば、足し算では\(5+7=12\)であるとか、\(3+(-1)=2\)であるとかのように2つの元に対して、ただ1つの元が決まるような写像を考えることができます。この場合には、2つの整数から1つの整数への写像ということで、\(f:\mathbb{ Z }\times \mathbb{ Z } \rightarrow \mathbb{ Z }\)と表現することができます。このような集合の直積に対する写像を考えることもできます。
\(5+7=12\)の場合、\( f:(5,7) \mapsto 12\)という写像と考えられます。
単射・全射・全単射
単射
はじめに単射ではない例を紹介します。\(A=\{小盛,並盛,アタマの大盛,サラシア牛丼並盛,大盛,特盛,超特盛\}\)とすると
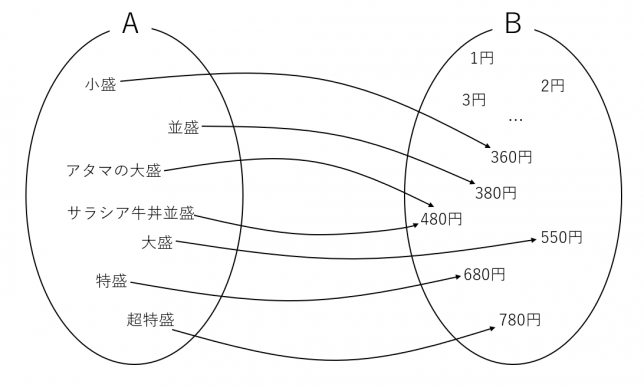
となり、2つの商品が同価格480円となってしまいます。このように図を描いたときに、矢の先が同じところに向かってしまう場合は単射とはいいません。最初の例のように、

と矢の先が同じところに向かない場合、単射(一対一の写像)といいます。数式で書くと
\( ( \forall a \in A) ( \forall a’ \in A) ( x \neq x’ \Rightarrow f(x) \neq f(x’) ) \)
となります。言葉で書くと、「集合Aから任意の元を2つ取った場合、その2つが異なれば行先も異なる」といった感じでしょうか。
全射
次に、全射について書きます。上の図で、金額の集合\(B\)には、1円、2円…といった金額が含まれていますが、その価格の商品はありません。集合\(B\)に到達する矢印が網羅されていません。このような場合は、全射ではありません。集合\(B\)を限定してみましょう。
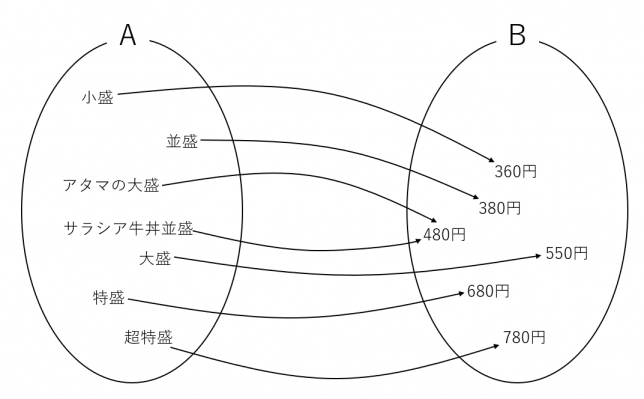
集合\(B\)の元を限定すると、必ず集合\(B\)にたどり着くようになりました。このように、集合\(B\)に必ず到達するような写像を全射(上への写像)といいます。数式で書くと
\( ( \forall b \in B) ( \exists a \in A) b=f(a) \)
となります。「任意の集合\(B\)の元\(b\)には、\(b=f(a)\)となる集合\(A\)の元が必ず存在する」ということになります。
全単射
次は全単射です。全射でありかつ単射である写像のことです。全単射という表現だけでなく、双射であるとか一対一対応という表現で書かれる場合もあります。上の例でサラシア牛丼並盛を除くと全単射になります。
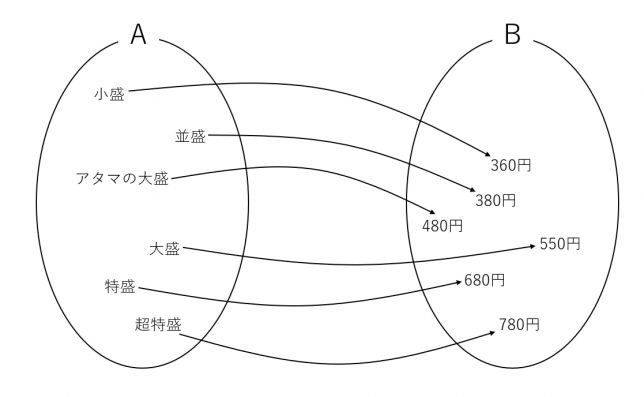
逆写像
ここまでは、集合\(A\)から集合\(B\)への対応について考えてきました。逆方向の対応として、集合\(A\)から集合\(B\)への写像が全単射である場合には、集合\(B\)から集合\(A\)への対応というのも考えられます。これを\(f^{-1}:A \rightarrow B\)と表し、逆写像といいます。
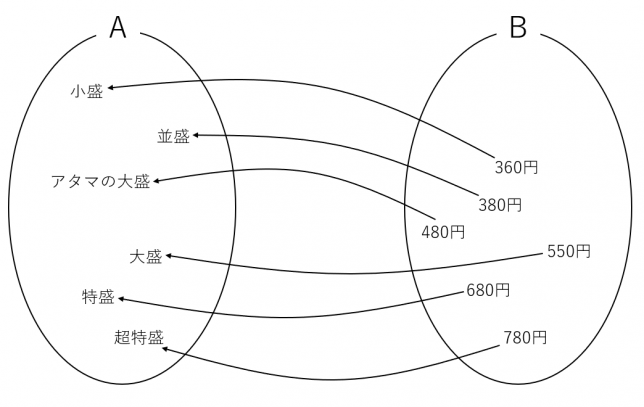
は先ほどの写像の逆写像になります。
まとめ
多少数式を交えて整理しましたが、押さえておくポイントを整理します。
- ある集合から別の集合に対応する操作の概念として写像の考え方は必要である。
- 集合の直積に対する写像というものもある。どのような集合の組合せに対して対応付けを考えてるかを明確にした方がよい。
- 一意に対応しているか、対応した先の集合が網羅されているかを意識することも必要である。
- 逆方向の対応付けが成立しているかを考えることも必要である。
程度のことを踏まえて、情報と情報の対応付けをどのように扱っていくかを考えていくことが重要ではないかと思っています。
今回はこれでおしまい。牛丼でも食べに行こうかな。それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません