情報科の目で見る数学科学習指導要領(6)状態遷移図

こんにちは。まだまだ、数学科の学習指導要領解説で扱われている内容を、情報科として扱うとどうなるかシリーズが続きます。今回のタイトルをどうするか迷いましたが、どちらかというと情報科学での名称を付けることにしました。
次期学習指導要領の数学A
数学科の学習指導要領で、注目された点の1つに「数列」と「ベクトル」が別々の科目に分かれたということがあります。これとも関連するのですが、数学を身の回りの事象や社会的な問題に活用しようという流れがあるようです。特に、数学A・数学B・数学Cでは顕著にその傾向があり、数学Aでは「数学と人間の活動」、数学Bでは「数学と社会生活」、数学Cでは「数学的表現の工夫」という項目が設けられています。また、統計分野との関わりから数学Bが大きく変更されたように思います。詳しくは、以前整理した次期学習指導要領の内容のページへのリンクを貼っておきます。
今回の題材として、数学Aの「数学と人間の活動」から情報科としても扱えるような内容を探っていきます。そもそも「数学と人間の活動」とは何なのかを確認しておきましょう。
(3) 数学と人間の活動
数学と人間の活動について,数学的活動を通して,それらを数理的に考察することの有用性を認識するとともに,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 数量や図形に関する概念などと人間の活動との関わりについて理解すること。
(イ) 数学史的な話題,数理的なゲームやパズルなどを通して,数学と文化との関わりについての理解を深めること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 数量や図形に関する概念などを,関心に基づいて発展させ考察すること。
(イ) パズルなどに数学的な要素を見いだし,目的に応じて数学を活用して考察すること。[内容の取扱い]
(3) 内容の(3)の指導に当たっては,数学的活動を一層重視し,生徒の関心や多様な考えを生かした学習が行われるよう配慮するものとする。
(4) 内容の(3)のアでは,整数の約数や倍数,ユークリッドの互除法や二進法,平面や空間において点の位置を表す座標の考え方などについても扱うものとする。
となっています。現行の学習指導要領で学習内容とされていた整数や基数についての内容は、ここでの内容になっているようです。二進法はデジタル表現の基本になっているのですが、これについては、きっと他のサイトで見つけられると思いますので、このサイトでは今すぐには取り上げないことにします。
状態遷移として扱える問題
それよりも、数理的なゲームやパズルでは、その時々の状況を何らかの方法で表す必要があります。いい換えれば、ゲームやパズルでの情報を表現する必要が生じることになります。ゲームやパズルでの状態についての情報を表現する方法として、状態遷移図というものがあります。何かをする度に、どのように変化していくかを有向グラフで表現するもので、状態をノード、遷移をエッジとして表します。
これが使える具体的な問題として、学習指導要領解説では、「油分け算」というなかなか楽しそうな例が示されています。
数学史的な話題としては,例えば,江戸時代に吉田光由が著した「塵劫記」の次のような問題を取り上げ,方程式などを利用して解き,その解の意味を考えたり,似たような問題がないか調べ,人間の活動に数学がどのように関わっているかを考察したりする活動を行うことが考えられる。他に,算額に見られる問題を取り扱うことも考えられる。
「一斗(十升)入りの桶に油が一斗入っている。七升枡と三升枡を使って,一斗桶と七升枡にそれぞれ五升ずつ油を分けたい。どのようにすればよいか。」(油分け算)
少し問題に補足を加えると、枡や桶には目盛りはありません。「容器があふれる直前まで移し替える」か、もしくは「容器に入っている量すべてを移し替える」だけの操作で五升ずつ油を分けたいという問題です。この移し替える手順の一部を状態遷移図で表してみます。
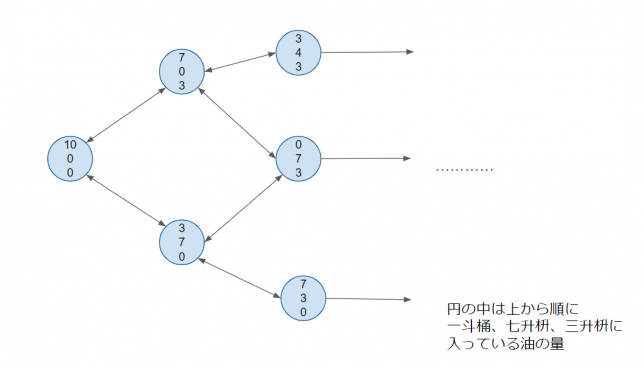
簡単に説明します。最初の状態は左端の(10,0,0)です。この数値は、(一斗桶,七升枡,三升枡)に入っている油の量を示しています。すべての油は一斗桶に入っていることを示しています。
次に、移し替える操作を行いますが、2つの操作が考えられます。一斗桶→三升枡、一斗桶→七升枡の2つです。一斗桶→三升枡の操作を行うと(7,0,3)、一斗桶→七升枡の操作を行うと(3,7,0)に状態が遷移します。このように、それぞれの状態ごとに遷移できる状態を調べて図にしていくと、目的の状態である(5,5,0)にたどり着きます。
上図では、操作を2回行ったところまでの状態遷移図を示しましたが、この問題はとても状態数が多くあり、図をうまく書かないとグチャグチャになってしまいます。そこで、横軸を七升枡、縦軸を三升枡に入っている油の量として、図を整理すると次の図になります。
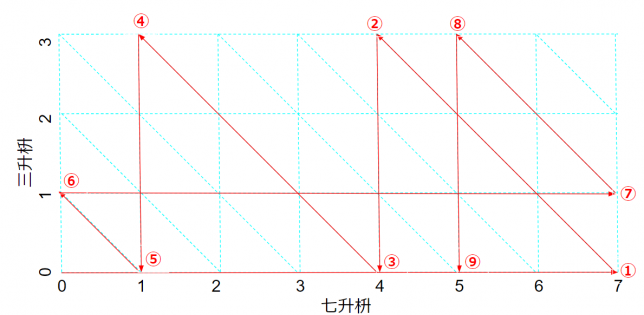
一斗桶の状態がないと思われる方がいるかもしれませんが、
一斗桶の油の量+七升枡の油の量+三升枡の油の量=一斗(十升)
ということから、
一斗桶の油の量=十升-(七升枡の油の量+三升枡の油の量)
により一意に一斗桶の油の量は決まるので大丈夫です。上図では、水色の点線の交点がノードになります。水平線は「一斗桶⇔七升枡」間の移し替え、垂直線は「一斗桶⇔三升枡」間の移し替え、右下がりの斜線は「七升枡⇔三升枡」間の移し替えになります。移し替えは、「容器があふれる直前まで移し替える」か、もしくは「容器に入っている量すべてを移し替える」だけの操作のため、ノード間の移動は、外枠の線に交わるまで移すことになります。(数学的に考える余地を残すために、水平線による状態遷移、垂直線による状態遷移、斜線による状態遷移、外周線に交わるまで移動しなければならないことの数学的な理由は書かないことにしておきます)
上記の図により(5,5,0)まで遷移する手順は、次のようになります。
手順0 初期状態 (10,0,0)
手順1 一斗桶 ⇒ 七升枡 (3,7,0)
手順2 七升枡 ⇒ 三升枡 (3,4,3)
手順3 三升枡 ⇒ 一斗桶 (6,4,0)
手順4 七升枡 ⇒ 三升枡 (6,1,3)
手順5 三升枡 ⇒ 一斗桶 (9,1,0)
手順6 七升枡 ⇒ 三升枡 (9,0,1)
手順7 一斗桶 ⇒ 七升枡 (2,7,1)
手順8 七升枡 ⇒ 三升枡 (2,5,3)
手順9 三升枡 ⇒ 一斗桶 (5,5,0)
により、目標の状態にたどり着きます。 もう1つ状態遷移図で解ける問題の例として、「河渡りの問題」が挙げられています。こちらは状態の数はそんなに多くならないので、紙とペンがあればできるので、やってみてください。
今回は短いですが、ここまでにします。プログラムを書こうかと思いましたが、またの機会にします。それではまた。











ディスカッション
コメント一覧
まだ、コメントがありません