ドラゴン曲線

こんにちは。今回はドラゴン曲線をタートルグラフィックスで描いてみます。なぜドラゴンカーブを描くかというと、とにかく描きだいからです。
どこに分類させるかとても迷いましたが、とりあえずプログラミングにしておきます。だけど、授業で使える教材にはならないですね・・・すみません<(_ _)>
ドラゴン曲線とは
ドラゴン曲線とは、帯状の紙を同じ方向に折り続けて、折り目が90°になるように開いてできる図形です。実際にやってみました。
1 帯状の紙を用意します

2 帯状の紙を半分に折り、更に半分に折り、更に半分に折り、・・・を繰り返します(写真では2回折っています)

3 折り目を90°開いた状態にします

このようにしてできた形がドラゴン曲線です。
3~4回くらいならば、実際に紙を折って作ることができますが、それ以上になると紙の厚みや折り返しの長さの問題で困難になります。
そこで、コンピュータを使って描いてみます。どこかで紙が交差しそうですが、案外交差しません。
ドラゴン曲線を描くプログラム
タートルグラフィックスで描いてみます。
import turtle
import math
kamepy = turtle.Turtle()
kamepy.speed(0)
size = kamepy.getscreen().screensize()
kamepy.penup()
kamepy.setx( - size[0] / 2 )
kamepy.pendown()
def dragon( generation , length , sign ):
if ( generation == 0 ):
kamepy.forward( length )
else:
kamepy.left( sign * 45 )
dragon( generation-1 , length / math.sqrt( 2 ) , 1 )
kamepy.right( sign * 90 )
dragon( generation-1 , length / math.sqrt( 2 ) , -1 )
kamepy.left( sign * 45 )
dragon( 2 , size[0] , 1 )
タートルグラフィックスを使って描いたドラゴン曲線
最後の行の1つ目の引数が折り返しの回数になっています。この値を変えていくつか描いてみました。
2回折り返したときのドラゴン曲線です。

3回回折り返したときのドラゴン曲線です。

4回折り返したときのドラゴン曲線です。
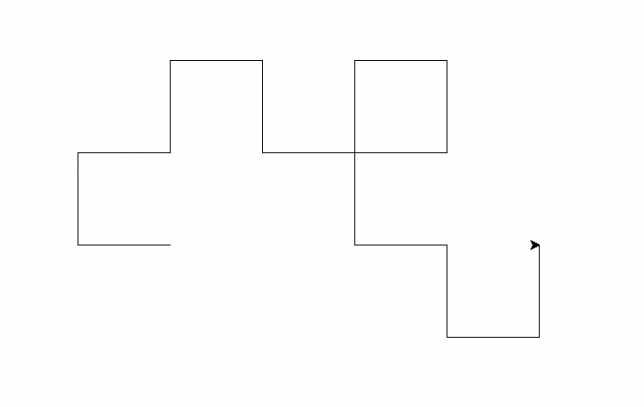
5回折り返したときのドラゴン曲線です。
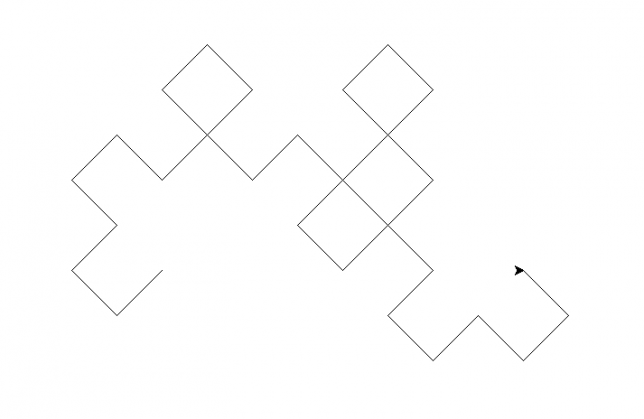
次は一気に飛んで、10回折り返したときのドラゴン曲線です。
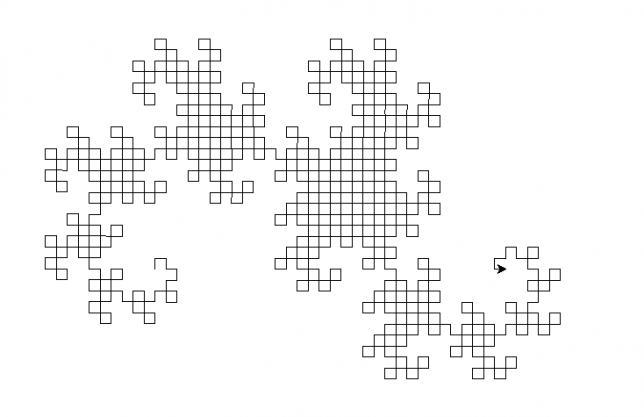
さらに飛びます。次は15回折り返したときのドラゴン曲線です。これを描き上げるまでものすごく時間がかかりました。

自分自身の中に相似な形が含まれています。さらにその中にも相似な形が含まれています。これを自己相似性といいます。
どちらかというとプログラムより図形を見てみたかったから記事として取り上げました。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません