情報科の目で見る数学科学習指導要領(3)Pythonのタートルグラフィックスでコッホ曲線(極限)

こんにちは。今回も、引き続き数学科の学習指導要領解説から題材を取り上げます。今回は数学Ⅲの極限という意外な(?)単元からになります。
学習指導要領解説から
学習指導要領解説には
数列や関数の値の極限に着目し,事象を数学的に捉え,コンピュータなどの情報機器を用いて極限を調べるなどして,問題を解決したり,解決の過程を振り返って事象の数学的な特徴や他の事象との関係を考察したりすること(イ(ウ))
具体的な事象について,漸化式を用いて表現したり,コンピュータなどの情報機器を用いたりして一般項や極限を調べ,問題解決したり,他の事象との関係を考察したりすることができるようにする。
例えば,「積み立てと複利計算」などを取り扱うことが考えられる。また,コッホ雪片やシェルピンスキーのギャスケットなどのフラクタル図形の周の長さや面積を求めることも考えられる。
とあります。コンピュータの活用については、現行の学習指導要領解説でもすべての教科で書かれているので、今回のシリーズとしてすべてを取り上げませんが、コッホ雪片やシェルピンスキーのギャスケットの図が掲載されているのが目に留まってしまいました。そんな理由で取り上げます。
コッホ雪片(コッホ曲線)とは
まずは、コッホ曲線の描き方を確認していきましょう。
1本の線分があります。
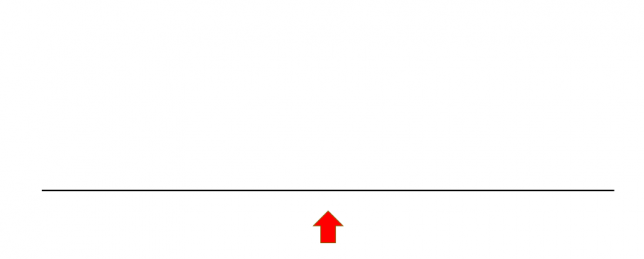
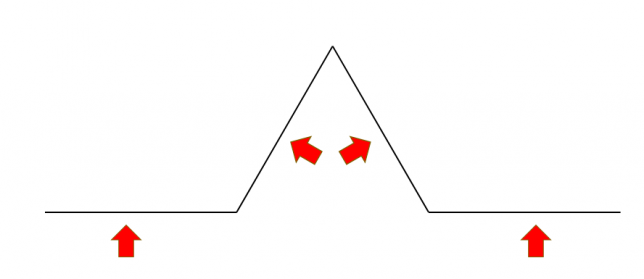
この線分を3等分します。3等分したうちの真ん中の線分が一辺になるような正三角形を作ります。元からあった辺は消してしまいます。これで1回の操作は完了です。
さらに上の図の4本の線分について、同じ操作を繰り返します。
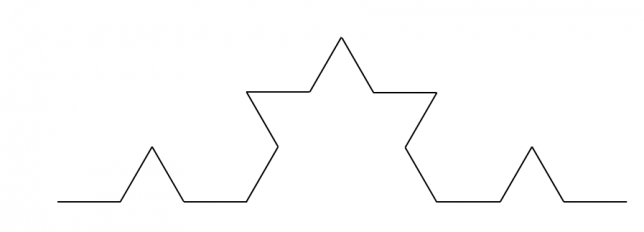
このようにしてできた図形をコッホ曲線といいます。この図形を120°、240°回転させたものとをつなぐと雪の結晶のような図形になります。
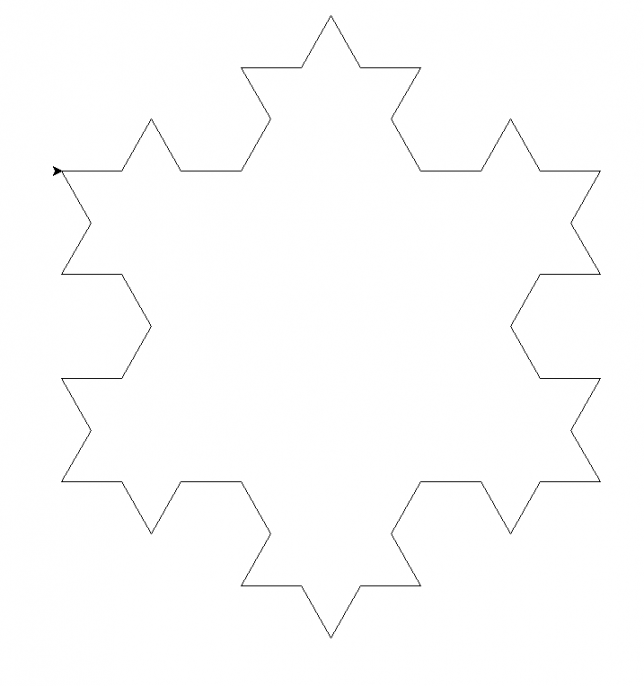
これをコッホ雪片といいます。確かに雪の結晶のように見えますね。これをきれいに手作業で描くのは大変なので、コンピュータを活用をして描くことにしましょう。極限を考えるためにも、一度はきれいに描かれた図を見て考えた方がよいと思います。
Pythonでのタートルグラフィックス
Pythonのタートルグラフィックスを使って描いてみましょう。手順としては次のようなものになります。
- 線分の長さをlengthとします。
- lengthの1/3にあたるひとまわり小さいコッホ曲線を描きます。
- 左に60°回転して、2つ目のひとまわり小さいコッホ曲線を描きます。
- 右に120°回転して、3つ目のひとまわり小さいコッホ曲線を描きます。
- 左に60°回転して、4つ目のひとまわり小さいコッホ曲線を描きます。
これでコッホ曲線が描けます。一回り小さいコッホ曲線は、この手順でlengthの値を元の1/3の値として描くことで描けます。さらに一回り小さいコッホ曲線は、この手順でlengthの値を小さいコッホ曲線のlengthの1/3の値として描くことで描けます。…(以下、繰り返し)…最も小さいコッホ曲線では、一回り小さいコッホ曲線を描くのではなく、直線を描くことにします。
マトリョーシカみたいな感じです。マトリョーシカみたいなものは、再帰を使うことで簡単にプログラムにできます。
この手順を3回繰り返すとコッホ雪片になります。
さて、そのプログラムを掲載します。
import turtle
import math
kamepy = turtle.Turtle()
kamepy.speed(0)
size = kamepy.getscreen().screensize()
kamepy.penup()
kamepy.setx( - size[1] )
kamepy.sety( size[0] / 2 )
kamepy.pendown()
def koch( generation , length ):
if ( generation == 0 ):
kamepy.forward( length )
else:
koch( generation-1 , length / 3 )
kamepy.left( 60 )
koch( generation-1 , length / 3 )
kamepy.right( 120 )
koch( generation-1 , length / 3 )
kamepy.left( 60 )
koch( generation-1 , length / 3 )
for i in range( 3 ) :
koch( 2 , size[0] * 1.5 )
kamepy.right( 120 )
まとめ
まとめとして、かなり細かいところまで描き込んだコッホ雪片を載せることにします。

今回はタートルグラフィックスで描いてみました。別の機会に座標を用いて描いてみたいと思います。
また、数学では極限での内容になっていますので、細かくし続けたときに、コッホ雪片の周の長さや面積の極限がどうなるかが興味の対象になるでしょう。図形は一定の範囲内で描くことができるので、面積はある値に収束しそうなことは予想できます。しかし、周の長さは収束するのでしょうか?言い換えると、タートルグラフィックスで有限時間で描けるのでしょうか?
興味は尽きないので、また機会があれば取り上げたいと思います。今日はこれでおしまい。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません