情報科の目で見る数学科学習指導要領（２）指数関数

2018-11-30モデル化とシミュレーション

こんにちは。引き続き、数学科の学習指導要領解説の中から、「情報科でやってみるとどうなるか調べてみよう！」シリーズです。２回目として、指数関数です。

数学科学習指導要領解説より

学習指導要領解説から題材を引用します。

ある薬を飲んだときの１時間後の薬の体内残量が80％であるとき，体内残量が50％以下になるのは薬を飲んでおよそ何時間後になるかを考える活動が考えられる。この際，変化の様子を捉えたり，対数の計算をしたりするために，コンピュータなどの情報機器を積極的に用いるようにする。さらには，体内残量の割合を変えたときに，体内残量が50％以下になる時間がどのように変化するかを発展的に考察する活動も考えられる。

ということで、薬を飲んだ後の体内の残量をシミュレーションしてみます。

薬の残量について

体内の残量が本当に指数関数になっているか気になったので、調べてみました。

純粋な指数関数ではなく、血中濃度が最高になるまで一定時間が必要で、そこから一定時間ごとに半減していくようです。さらに調べてみました。

注射で一気に血中濃度が最高になることもあるし、繰り返し飲む場合もあるし・・・どこまでリアリティを求めることにしましょうか。

モデル化

まず、計算式にしにくいところを省略します。薬を飲んでから最高血中濃度（Cmax）に達するまでの時間（\(T_{max}\)）は0とします。薬を飲んだら、すぐに血中に取り込まれるということにしてしまいます。

次に、学習指導要領解説では、薬を飲んでから１時間後の体内残量が８０％と書かれていますが、

のように、消失半減期（\(T_{1/2}\)）のように示されています。ここではリアリティを求めてみましょう。（一貫していないですね😅）指数関数にするには底を求める必要があります。

\[y=a^x\]

の指数関数で表現できるものとすると、体内残量が\(1/2\)になる時間が\(T_{1/2}\)なので

\[\frac{1}{2}=a^{T_{1/2}}\\a=\left(\frac{1}{2}\right)^\frac{1}{{T_{1/2}}}\]

で底\(a\)が求められます。これで指数関数になりました。次に時間間隔を決めます。薬を飲むのは１日に数回なので、あまり間隔を細かくする必要はないと考えて、１時間単位で変化を調べることにします。そうすることにより、１時間後の血中濃度は先ほど求めた底\(a\)倍になります。すなわち

\[時刻tにおける血中濃度=時刻(t-1)における血中濃度\times a\]

になります。

ここでシミュレーションを始めてもよいのですが、せっかくコンピュータを使ってシミュレーションしようとしているので、数学では求めにくいことをしてみましょう。薬は繰り返し飲みます。その変化も調べてみましょう。数式モデルを簡単にするために、一定時間ごとに服用することにします。そこで、パラメータとして服用間隔を設定してみます。それにより

\[時刻tにおける血中濃度=時刻(t-1)における血中濃度\times a\\+\mathrm{IF}(\mathrm{MOD}(時刻,服用間隔)=0,100,0)\]

という数式モデルが得られます。

シミュレーション

それでは表計算ソフトウェアを使ってシミュレーションしてみましょう。鎮痛などで使われるイブプロフェンで調べてみます。イブプロフェンでは、（\(T_{1/2}=1.86\)）のようです。これを24時間ごとに服用したときの血中濃度を調べてみます。

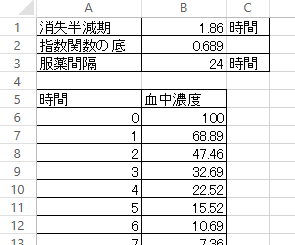
変化がわかるようにグラフを描いてみます。

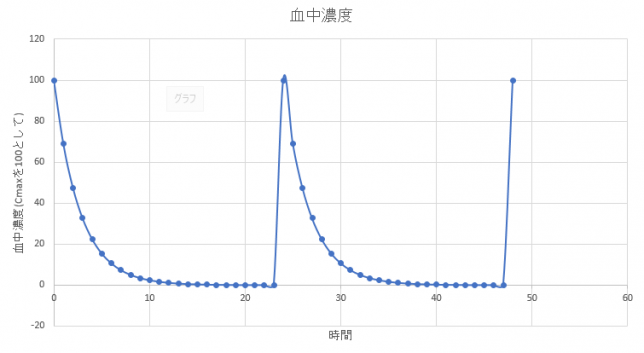
もう１例シミュレーションしてみます。（\(T_{1/2}=12\)）の薬を24時間ごとに飲み続けることをシミュレーションしてみます。

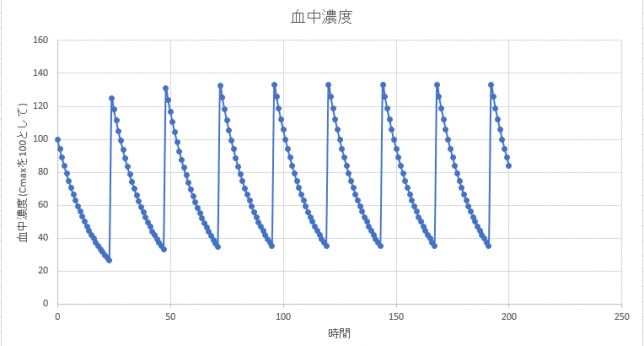
200時間経過までシミュレーションしてみました。消失半減期が長いので、常にCmaxの35%～130%程度の範囲の薬が体内に残留していることになります。翌日に薬を飲むときに、薬が体内に残留しているからといって、どんどん増え続けるということはなく、一定範囲に収まることがわかります。このように一定量体内にとどめておき、薬の効果が持続するように服用する薬もあるようです。

補足

コンピュータでシミュレーションできてしまうという理由で数学不要論を語るつもりは全くありません。今回の記事をもう一度読み直してください。よく読むと、モデル化で指数関数の底を求める計算については、分数の指数という指数関数（累乗根）の知識がなければ式変形できません。数式を活用することとコンピュータを活用することの相乗効果により、このようなシミュレーションができるようになると思います。

今回はこれでおしまいにします。それではまた。