テキサスホールデムのルールでポーカーをしたときの役ができる確率

こんにちは。前回は,トランプで5枚のカードを引いたときの役ができる確率を求めました。
実は,調べていて気になったことがあります。
テキサスホールデムという遊び方があり,その場合の役ができる確率が気になってしまったのです。
ということで,シミュレーションすることにより,大まかな確率を求めていきます。
テキサスホールデムとは
リンクを貼ろうと思ったのですが,案外ゲームの流れを説明したページばかりが見つかるので,自分で大まかに書くことにします。
裏向きに配られたプレーヤー手持ちのカード2枚と,テーブルに表向きに配られた5枚のカードの計7枚のカードでポーカーの役を作って,その役の強さを競うといった感じになります。
説明を書いたサイトでは,本格的にチップの賭け方や駆け引きなどの説明が載っているので,説明が難しいのですが,基本的にはこんな感じです。
それでは,シミュレーションしてみます。
シミュレーションしてみた
相変わらずExcelでシミュレーションしてみます。
ファンクションキーに重りを乗せたまま延々と再計算させてしまったので,なんと50万回ものシミュレーションになりました。
まずは,トランプをシャッフルします。
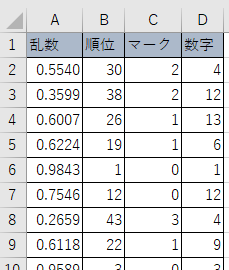
次に,7枚のカードが何であるかを調べています。
右側の計は数字ごとの枚数,下側の計はマークごとの枚数を表しています。
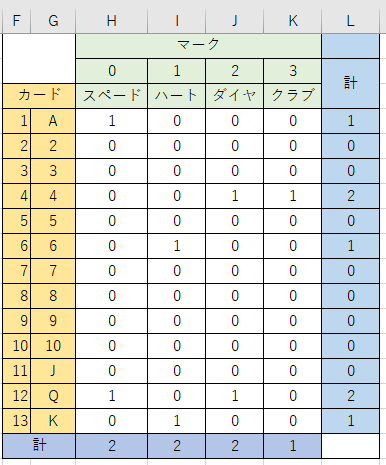
それでは,どのような役ができたか調べてみます。
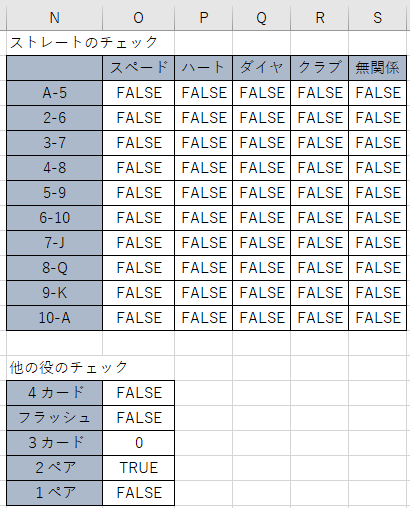
実は,ストレートフラッシュの判定を何回も間違えていました。
はじめは同じマークが5枚以上かつ連続した数字をストレートフラッシュと判定しまいましたが,それだとものすごく高確率で出現してしまい,見直しました。
ちゃんとマークと数字を見なければ判定できないことがわかり,前回の判定をすべて捨てて式を作り直しました。(式は次回に示します)
50万回シミュレーションしてみた結果,どの程度それぞれの役が出現したか集計しました。
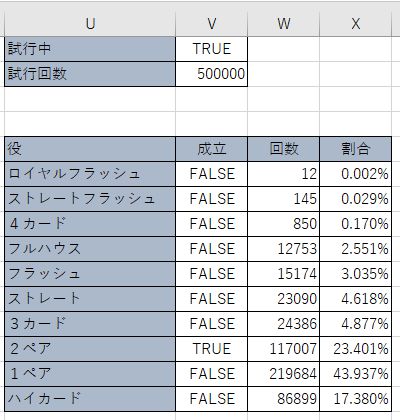
50万回もシミュレーションしてみた甲斐もあって,なんとロイヤルフラッシュが12回も出ました!
ちなみに,5枚だけでできる役と7枚使ってできる役のシミュレーション結果を比較してみます。
なお,5枚だけでできる役は前回の5万回シミュレーションした結果になります。
| 役 | 5枚だけ | 7枚 |
| ロイヤルフラッシュ | 0.000% | 0.002% |
| ストレートフラッシュ | 0.000% | 0.029% |
| 4カード | 0.028% | 0.170% |
| フルハウス | 0.162% | 2.551% |
| フラッシュ | 0.224% | 3.035% |
| ストレート | 0.394% | 4.618% |
| 3カード | 2.310% | 4.877% |
| 2ペア | 4.764% | 23.401% |
| 1ペア | 41.696% | 43.937% |
| ハイカード | 50.422% | 17.380% |
もちろんほとんどの役ができる確率は上がるのですが,2枚増えるだけでちゃんとポーカーらしいゲームができそうです。
今回はこれでおしまいにします。それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません