情報科の目で見る数学科学習指導要領(9)離散グラフ

こんにちは。まだまだ数学科との関係について書くシリーズが続きます。「数学I」「数学Ⅱ」「数学Ⅲ」「数学A」「数学B」と順に進めてきて,いよいよ最後の「数学C」まできました。大詰めです。「平面上の曲線と複素数平面」にスピログラフが取り上げられていますが,別の機会に取り上げることにします。今回は「数学的な表現の工夫」に書かれている離散グラフを取り上げることにします。
離散グラフとは
離散グラフを知らない人は,駅のきっぷ売り場に貼ってある路線図を考えてもらうとよいと思います。路線図が「離散グラフ」になります。そこに描かれている「駅」に相当するものを丸で表現し,「頂点(またはnodeとかvertex)」といいます。駅間を結ぶ線路に相当する線を「辺(edge)」といいます。鉄道の路線図だけでなく,道路のつながりやSNSのフォロー・フォロワーの関係など,つながりを表すことは多くあります。実際の場面を考えると,離散グラフの出番は多いことがわかると思います。
例としてJR東日本の新潟近郊区間を使うことにします。
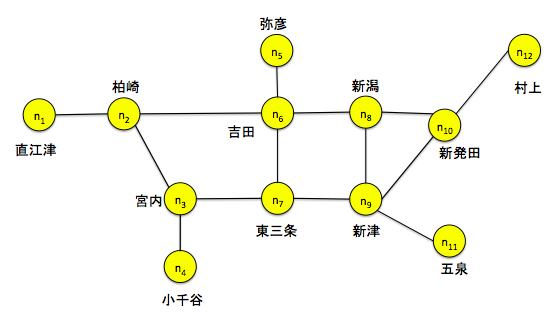
離散グラフの種類
無向グラフと有向グラフ
つながりには単純に接続しているものと,一方通行やSNSのつながりのように方向性があるものとがあります。単純なつながりは,特に向きがないので無向グラフといいます。無向グラフでは,辺を線分で表現します。それに対して,一方通行のような方向性があるものを有向グラフといいます。図で表現する場合には,矢印で表現します。
重み付きグラフ
辺には向きだけではなく,辺の長さや大きさがあります。例えば道路を表現するには,距離が関わってきますし,有料道路などを考えると通行料金など辺ごとに値を持つことがあります。このように辺ごとに数値をもつような離散グラフを重み付きグラフといいます。方向性を考えると,重み付き無向グラフ・重み付き有向グラフがあります。
先ほどの新潟近郊区間の路線図の重みとして,距離を載せました。
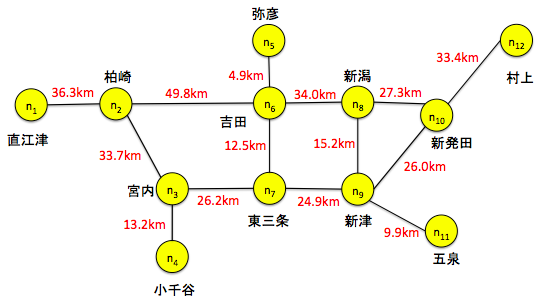
離散グラフのデータ表現(1)隣接行列
離散グラフは図で表現するのは比較的簡単ですが,コンピュータ上で離散グラフを扱うためには何らかのデータ形式で表現する必要があります。行と列にすべての頂点を配置します。
重みがない場合には,つながっている場合には成分を1,つながっていない場合には成分を0と表現すると2次元配列を使って表現することができます。重みがある場合には,成分を重みにします。隣接行列の利点は成分を確かめることで接続しているか否かがすぐに分かります。
例として新潟近郊区間について、重み付き隣接行列で表現してみました。
\[ \begin{bmatrix}
0 & 36.3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
36.3 & 0 &33.7 & 0 & 0 & 49.8 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 33.7 & 0 & 13.2 & 0 & 0 & 26.2 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 13.2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 4.9 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 49.8 & 0 & 0 & 4.9 & 0 & 12.5 & 34.0 & 0 & 0 & 0 & 0 \\
0 & 0 & 26.2 & 0 & 0 & 12.5 & 0 & 0 & 24.9 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 34.0 & 0 & 0 & 15.2 & 27.3 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 24.9 & 15.2 & 0 & 26.0 & 9.9 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 27.3 & 26.0 & 0 & 0 & 33.4 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 9.9 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 33.4 & 0 & 0 \end{bmatrix} \]
これをPythonで表現してみました。
stations = [ '直江津', '柏崎', '宮内' , '小千谷',\
'弥彦' , '吉田', '東三条',\
'新潟' , '新津', '新発田', '五泉', '村上' ]
route = \
[ [ 0, 36.3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],\
[36.3, 0, 33.7, 0, 0, 49.8, 0, 0, 0, 0, 0, 0 ],\
[ 0, 33.7, 0, 13.2, 0, 0, 26.2, 0, 0, 0, 0, 0 ],\
[ 0, 0, 13.2, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],\
[ 0, 0, 0, 0, 0, 4.9, 0, 0, 0, 0, 0, 0 ],\
[ 0, 49.8, 0, 0, 4.9, 0, 12.5, 34.0, 0, 0, 0, 0 ],\
[ 0, 0, 26.2, 0, 0, 12.5, 0, 0, 24.9, 0, 0, 0 ],\
[ 0, 0, 0, 0, 0, 34.0, 0, 0, 15.2, 27.3, 0, 0 ],\
[ 0, 0, 0, 0, 0, 0, 24.9, 15.2, 0, 26.0, 9.9, 0 ],\
[ 0, 0, 0, 0, 0, 0, 0, 27.3, 26.0, 0, 0, 33.4 ],\
[ 0, 0, 0, 0, 0, 0, 0, 0, 9.9, 0, 0, 0 ],\
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 33.4, 0, 0 ] ]
def distance( station1, station2 ):
return route[stations.index( station1 )][stations.index( station2 )]
def is_connected( station1, station2 ):
return bool( distance( station1 , station2 ) )
print( distance( '新潟' , '新津') )
print( is_connected( '柏崎', '吉田') )
print( is_connected( '新潟', '弥彦') )
出力結果は次のようになります。
15.2
True
False
隣接行列の問題点
隣接行列は,行と列にそれぞれ頂点を並べて,接続があるものに重みを付けたり,接続している目印として1を付けたりして表現していました。そのため,とてもわかりやすいのですが,頂点の数が増えてくると必ずしも接続しているとは限りません。むしろ接続していない頂点の方が圧倒的に多くなります。このような離散グラフを隣接行列で表現すると,ほとんどの成分が0になってしまいます。このようなほとんどの成分が0である行列を疎行列といいます。先の新潟近郊区間の隣接行列では、0でない要素は全144要素中28要素しかなく、疎行列になっていることがわかります。
鉄道網をさらに拡大して全国の鉄道網を隣接行列で表現することを考えてみます。駅の数は全国で9000を超えるそうです。何の工夫もしないで隣接行列で表現する場合,9000×9000=8100万個の要素が必要になります。しかし多くの駅は,一つの路線の途中駅です。両隣の駅と接続することを表す成分は0ではありませんが,残りの約9000の駅との成分は0で膨大なメモリの無駄遣いになります。
また、両端が同じ辺がある場合には表現が難しくなる点も問題点として挙げられます。
離散グラフのデータ表現(2)隣接リスト
それでは,メモリが無駄にならないよう表現方法を工夫することを考えます。
そもそも大多数の他の頂点とはつながっていなく,逆につながっている頂点は限られているので,つながっている頂点をリスト形式でデータを表現することにしましょう。
route = {
'直江津' : {'柏崎': 36.3},
'柏崎' : {'直江津': 36.3, '宮内': 33.7, '吉田': 49.8},
'宮内' : {'柏崎': 33.7, '小千谷': 13.2, '東三条': 26.2},
'小千谷' : {'宮内': 13.2},
'弥彦' : {'吉田': 4.9},
'吉田' : {'柏崎': 49.8, '弥彦': 4.9, '東三条': 12.5, '新潟': 34.0},
'東三条' : {'宮内': 26.2, '吉田': 12.5, '新津': 24.9},
'新潟' : {'吉田': 34.0, '新津': 15.2, '新発田': 27.3},
'新津' : {'東三条': 24.9, '新潟': 15.2, '新発田': 26.0, '五泉': 9.9},
'新発田' : {'新潟': 27.3, '新津': 26.0, '村上': 33.4},
'五泉' : {'新津': 9.9},
'村上' : {'新発田': 33.4}
}
print(route['新潟']) # 新潟につながっている駅
print(route['新津']['新発田']) # 新津と新発田の距離
print('小千谷' in route['吉田']) # 吉田と小千谷がつながっているか判定
出力結果は次のようになります。
{'吉田': 34.0, '新津': 15.2, '新発田': 27.3}
26.0
False
学習指導要領解説には、さらに「最短経路の探索」などを扱うことも考えられると書かれています。最短経路の探索は、いくつかアルゴリズムがあるので別の機会に扱います。
これでひととおり数学科の全科目について、学習指導要領解説から情報科と連携を図ることができる題材について見終わりました。まだ若干触れていない題材もありますが、また機会を改めて書きたいと思います。今回の数学科の学習指導要領解説から題材を探すシリーズは一区切りつけておしまいにします。
それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません