情報科の目で見る数学科学習指導要領(4)Pythonでニュートン法と二分法(極限)

こんにちは。今回も数学科の学習指導要領解説から題材を取り上げます。このサイトは「情報科 いっぽ まえへ!」という名前の高等学校の情報科を題材としているはずなのですが、延々と数学の題材を取り上げています。「本当に情報科のサイトなの?」と思ってくれるような定期購読者はいないようなので、気にしないでもう少し続けます。
情報科の学習指導要領解説から
珍しく情報科の学習指導要領解説から関連する項目を引用します。
ア(ア) コンピュータや外部装置の仕組みや特徴,コンピュータでの情報の内部表現と計算に関する限界について理解することでは,コンピュータの特性を踏まえて活用するために,コンピュータの基本的な構成や演算の仕組み,オペレーティングシステムによる資源の管理と入力装置や出力装置などのハードウェアを抽象化して扱う考え方,コンピュータ内部でのプログラムやデータの扱い方,値の範囲や精度について理解するようにする。その際,ソフトウェアはオペレーティングシステムの機能を利用して動作していること,コンピュータでは定められたビット数のデータが扱われ,表現できる値の範囲や精度が有限であることで,計算結果は原理的に誤差を含む可能性があることなどを理解するようにする。
イ(ア) コンピュータで扱われる情報の特徴とコンピュータの能力との関係について考察することでは,コンピュータの特性を踏まえて活用するために,コンピュータの能力を適切に判断する力,精度とデータ容量のトレードオフの関係などを踏まえ,コンピュータを適切に活用する力を養う。その際,計算などによって意図しない結果が生じたときに,データの扱い方や精度,計算の手順などに目を向けて改善しようとする態度を養うことが考えられる。(以下略)
というように、誤差や精度についてコンピュータを活用する際には考慮する必要があることを学びます。
数学科の内容として取り上げるものは、二分法とニュートン法になります。これらが関連する内容は数学Ⅲになるので、情報科と数学科が直接連携は難しいかもしれません。それでも、高等学校の範囲内どうしの内容になるので、誤差や精度の題材として取り上げます。
学習指導要領の単元的には「プログラミング」のようですが、コンピュータ内部でのデータの扱い方に関する内容ということで、今回の記事のカテゴリーは「情報のディジタル化」としておきます。
ニュートン法
数学Ⅲの課題学習として次のように書かれています。
数列の極限を事象の考察に活用できるようにする。
例えば,\(\sqrt{2}\)が漸化式\(a_{n+1}=\frac{a_{n}}{2}-\frac{1}{a_{n}} , a_{1}=2\)で定義される数列\(\{a_{n}\}\)の極限であることを用いて,\(\sqrt{2}\)の近似値を求めることを取り扱う。この応用として,ニュートン法による方程式の解の近似計算について文献により調査してみる。関数\(f (x)\)に関するニュートン法とは,適切な初項 を選び,漸化式\(a_{n+1}=a_{n}-\frac{f(a_{n})}{f'(a_{n})}\)によって定義される数列の極限を考えることにより,方程式 \(f(x)=0\)の解の 1 つを近似的に求める方法である。\(f(x)=x^2-2\)とすれば前述の漸化式を得ることができる。コンピュータなどの情報機器を用いて,実際に方程式の解の近似計算をするプログラムを制作することも考えられる。発展的には,3次以上の方程式の解の近似値を求めたり,初項の選び方によって収束値が変わるかどうかの考察を行ったりすることが考えられる。
このように、ニュートン法について書かれています。ニュートン法の説明がほとんどなく、突然漸化式が示されているので、教科書で取り上げることを想定しているのか、生徒が調べることを想定しているのかわかりませんが、このサイトにたどり着く高校生もいるかもしれませんので、概略だけ示したいと思います。
\(\sqrt{2}\)の近似値を求めたいと考えています。\(f(x)=x^2-2\)という二次関数と\(x\)軸との交点のうち、\(x\)座標が正の方の\(x\)座標が\(\sqrt{2}\)になります。この\(x\)座標を近似的に求める方法として、次のことを考えます。
\(\sqrt{2}\)に比較的近い\(x\)座標として\( a_{1}=2\)を取ります。関数\(y=f(x)\)上の点\((a_{1},{a_{1}}^2)\)における接線の方程式を求めると
\[y-2=2a_{1}(x-a_{1})\]
です。この接線と\(x\)軸との交点を求めると、\(x\)座標は\(x=\frac{3}{2}\)です。この\(x\)座標を\(a_{2}\)とします。
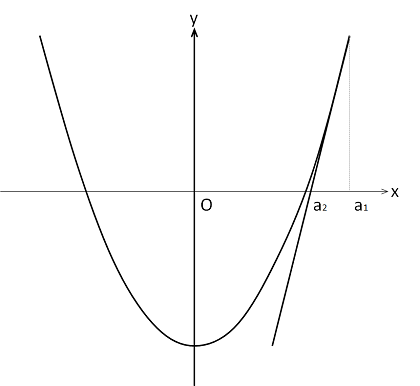
同様に、関数\(y=f(x)\)上の点\((a_{2},{a_{2}}^2)\)における接線の方程式を求めると\(y-2=2a_{2}(x-a_{2})\)であり、この接線と\(x\)軸との交点を求め、\(x\)座標を\(a_{3}\)とします。
以下この操作を繰り返し行い\(n \to \infty\)とすることにより、多くの場合二次関数\(f(x)=x^2-2\)と\(x\)軸との交点である\(\sqrt{2}\)に\(a_{n}\)が収束します。このようにして近似解を求める方法をニュートン法といいます。
一般化して、方程式\(f(x)=0\)の近似解を求めるには、次のようになります。
関数\(y=f(x)\)上の点\((a_{n},f({a_{n}}))\)における接線の方程式を求めると
\[y-f(a_{n})=f'(a_{n})(x-a_{n})\]
となります。この接線と\(x\)軸との交点の\(x\)座標\(a_{n+1}\)は
\[0-f(a_{n})=f'(a_{n})(a_{n+1}-a_{n})\\a_{n+1}=a_{n}-\frac{f(a_{n})}{f'(a_{n})}\]
となります。これを漸化式として、
\[\displaystyle \lim_{ n \to \infty } a_{n}\]
が収束する場合、方程式\(f(x)=0\)の近似解になります。「収束する場合」と書いているのは、「収束しない場合」もあるためです。
二分法
こちらは学習指導要領解説には登場しません。しかし、ニュートン法が収束しない場合もあり得るため、確実に求められるアルゴリズムとの比較をした方がよいと考えられます。そこで、二分法ならば高校数学の範囲内になります。
関数の値の極限について理解すること(ア(オ))
(略)
関連して関数の連続性についても取り扱う。特に,指数関数と対数関数については,定義域内の任意の値に対して連続であることを,コンピュータなどの情報機器を用いるなどして直観的に理解できるようにする。
と数学Ⅲの極限で書かれているので、次期学習指導要領でも数学Ⅲに「関数の連続性」「中間値の定理」は残ると考えられます。これらが二分法により近似解を求める根拠になります。
それでは二分法の説明をします。
二次関数\(f(x)=x^2-2\)において、\(f(1)=-1<0\)と負になるので、\(a=1\)とします。また、\(f(2)=2>0\)と正になるので、\(b=2\)とします。
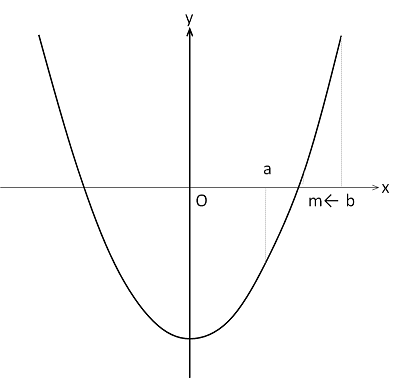
二次関数\(f(x)=x^2-2\)は、閉区間\([a,b]\)で連続であり、\(f(a)<0 かつ f(b)>0\)で中間値の定理より閉区間\([a,b]\)において\(x\)軸と交わります。この区間を少しずつ狭くしていきます。
\(m=\frac{a+b}{2}\)とします。ここで、\(m<0\)のとき、新しい\(a\)を\(m\)とします。また、\(m>0\)のとき、新しい\(b\)を\(m\)とします。これにより、定めた\(a,b\)に対しても、\(f(a)<0 かつ f(b)>0\)は成り立ちます。この\(a,b\)に対して、同様に\(m=\frac{a+b}{2}\)を求めることを繰り返していきます。徐々に閉区間\([a,b]\)が狭くなり、近似解が求まります。
イメージとして捉えると、中点を使いながら「はさみうち」にしていく感じになると思います。
Pythonでニュートン法を使ってみる
それでは、Pythonのプログラムを掲載します。epsilonは収束したかどうかを判定するための値になります。
def new_a(a):
return a/2 + 1/a
i = 1
a = 2
olda = 4 # aと等しくない値を仮の値とする
epsilon = 0.0000000000000005
while abs( olda - a ) > epsilon:
print( 'a[' + str( i ) + '] = ' + str( a ) )
olda = a
a = new_a( a )
i+=1
print( 'a[' + str( i ) + '] = ' + str( a ) )
実行結果を掲載します。
a[1] = 2
a[2] = 1.5
a[3] = 1.4166666666666665
a[4] = 1.4142156862745097
a[5] = 1.4142135623746899
a[6] = 1.414213562373095
a[7] = 1.414213562373095
かなり早く収束します。
Pythonで二分法を使ってみる
こちらも、Pythonのプログラムを掲載します。
def f( x ):
return x**2 - 2
def mid( a , b ):
return ( a + b ) / 2
i = 1
a = 1
b = 2
epsilon = 0.0000000000000005
while abs( b - a) > epsilon:
print( 'i:' + str( i ) + ' a=' + str( a ) + ' b=' + str( b ) )
m = mid( a , b )
if f( m ) < 0:
a = m
else:
b = m
i += 1
print( 'i:' + str( i ) + ' m=' + str( mid( a , b ) ) )
epsilonの値を0にすると、無限ループになってしまいます。これは、a=1.414213562373095,b=1.4142135623730951となった先では、a=bとはならず桁が落ちることが繰り返されてしまうためです。このような小数の桁落ちを体験してみるということも、コンピュータ内部での情報の表現を考えるきっかけの一つになるのではないでしょうか。
実行結果として、上のepsilonを使ったときのものを示します。
i:1 a=1 b=2
i:2 a=1 b=1.5
i:3 a=1.25 b=1.5
i:4 a=1.375 b=1.5
i:5 a=1.375 b=1.4375
i:6 a=1.40625 b=1.4375
i:7 a=1.40625 b=1.421875
i:8 a=1.4140625 b=1.421875
i:9 a=1.4140625 b=1.41796875
i:10 a=1.4140625 b=1.416015625
i:11 a=1.4140625 b=1.4150390625
i:12 a=1.4140625 b=1.41455078125
i:13 a=1.4140625 b=1.414306640625
i:14 a=1.4141845703125 b=1.414306640625
i:15 a=1.4141845703125 b=1.41424560546875
i:16 a=1.4141845703125 b=1.414215087890625
i:17 a=1.4141998291015625 b=1.414215087890625
i:18 a=1.4142074584960938 b=1.414215087890625
i:19 a=1.4142112731933594 b=1.414215087890625
i:20 a=1.4142131805419922 b=1.414215087890625
i:21 a=1.4142131805419922 b=1.4142141342163086
i:22 a=1.4142131805419922 b=1.4142136573791504
i:23 a=1.4142134189605713 b=1.4142136573791504
i:24 a=1.4142135381698608 b=1.4142136573791504
i:25 a=1.4142135381698608 b=1.4142135977745056
i:26 a=1.4142135381698608 b=1.4142135679721832
i:27 a=1.414213553071022 b=1.4142135679721832
i:28 a=1.4142135605216026 b=1.4142135679721832
i:29 a=1.4142135605216026 b=1.414213564246893
i:30 a=1.4142135605216026 b=1.4142135623842478
i:31 a=1.4142135614529252 b=1.4142135623842478
i:32 a=1.4142135619185865 b=1.4142135623842478
i:33 a=1.4142135621514171 b=1.4142135623842478
i:34 a=1.4142135622678325 b=1.4142135623842478
i:35 a=1.4142135623260401 b=1.4142135623842478
i:36 a=1.414213562355144 b=1.4142135623842478
i:37 a=1.4142135623696959 b=1.4142135623842478
i:38 a=1.4142135623696959 b=1.4142135623769718
i:39 a=1.4142135623696959 b=1.4142135623733338
i:40 a=1.4142135623715149 b=1.4142135623733338
i:41 a=1.4142135623724243 b=1.4142135623733338
i:42 a=1.414213562372879 b=1.4142135623733338
i:43 a=1.414213562372879 b=1.4142135623731065
i:44 a=1.4142135623729928 b=1.4142135623731065
i:45 a=1.4142135623730496 b=1.4142135623731065
i:46 a=1.414213562373078 b=1.4142135623731065
i:47 a=1.4142135623730923 b=1.4142135623731065
i:48 a=1.4142135623730923 b=1.4142135623730994
i:49 a=1.4142135623730923 b=1.4142135623730958
i:50 a=1.414213562373094 b=1.4142135623730958
i:51 a=1.414213562373095 b=1.4142135623730958
i:52 a=1.414213562373095 b=1.4142135623730954
なんと収束するまで、52回もかかってしまいました。さらなる探究として、収束速度の比較について考えてみるのもよいかと思います。
それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません