表計算ソフトウェアでシミュレーション（４）待ち行列のシミュレーション①とりあえずシミュレーションしてみた
こんにちは。今回は待ち行列のシミュレーションをしていきます。
お客さんが来る時刻を決める
前回、お客さんが来る分布が指数分布になっていることをまとめました。
https://joho-ka.mints.ne.jp/simulation-with-spreadsheet-03結果として、前の人との差ごとに確率と累積確率を表にまとめて、それを使うことにしました。
この表を使って、お客さんが来る時刻を作ってみましょう。
まず、乱数を発生させます。
=rand()
次に、表と対応する秒数に変換して、前の人との差を秒数で求めます。
=vlookup(乱数,表,2)
表の部分は絶対参照にしておきましょう。
次に、店に来る時刻を求めます。
前の人との差を求めていたので、前の人が店に来た時刻に足せば求められます。すべてのお客さんに対して同じ式で計算できるように、０人目を作っておいて、０人目が店に来た時刻を０にしておくのがミソです。
すると
=前の人が店に来た時刻+前の人との差
という式で統一できます。
これで、お客さんがいつ店にやって来るかが決まりました。
お客さんが注文するものを決める
次に、お客さんが注文するものを決めます。
そのためには、この店のメニューが必要です。
うどん・そば・ラーメン・カレー・定食と５種類のメニューがあることとします。
また、これらはお客さんが注文してから作ることにします。
この数値が妥当かどうかわかりませんが、とりあえず下の表のようにします。
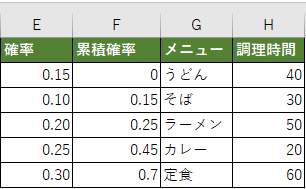
乱数を発生させて、この表と対応付けることにします。
乱数は、
=rand()
注文したものと調理時間はそれぞれ
=vlookup(乱数,表,2)
=vlookup(乱数,表,3)
で求められます。
注文できる時刻と料理を受け取る時刻を求める
これで、お客さんの行動が決まったので、注文できる時刻と料理を受け取る時刻を求めます。
注文できる時刻を求めるのは少し難しいです。
注文できる時刻
① 前の人がすでに料理を受け取っている場合
この場合には、待たされることなく店に到着した時刻に注文することができます。
② 前の人がまだ料理を作ってもらっている場合
次に、自身が店に到着した時刻に、前の人がまだ料理を受け取っていない場合です。
この場合は、前の人が料理を受け取るまで待ち、終わった時刻に注文することができます。
①または②のいずれかしかないので、場合分けはこれで十分です。
注文できる時刻を考えるには、前の人が料理を受け取る時刻と、自身が店に到着する時刻を比較すればよさそうです。
場合分けというと、if っぽいのですが、2つの時刻のうち時刻の遅い方になります。時刻が遅いということは数値が大きくなるので、実は max で最大値を求めればよいのです。
そうすると
=max(前の人の受取時刻,自分自身の到着時刻)
で求めることができます。
ここでも、0人目の受取時刻を０にしておくことで、全員の計算式をそろえることができます。
料理を受け取る時刻
これは難しくありません。
注文してから、調理してもらう時間がかかって受け取るので、
=注文時刻+調理時間
です。
待ち時間を求める
最後に待ち時間を求めます。
ここで、何をもって待ち時間と呼ぶかが問題ですが、店に到着してから注文できるまでの時間を待ち時間と呼ぶことにします。
調理して料理が出てくるまでの時間も待たされるのですが、自分で調理時間が長いものを頼んで「待たされた！」というのは、何か違うような気がするので、先ほどの解釈で計算します。
ということで
=注文時刻 – 到着時刻
になります。
まとめ
ここまで考えてきた数式を、表計算ソフトウェアで計算させてみます。
という表により、お客さんの様子をシミュレーションし、待ち時間を求めることができるようになりました。
今回はこれでおしまいにします。それではまた。