表計算ソフトウェアでシミュレーション(3)お客さんはいつ来るの?それは指数分布のようです

こんにちは。この表計算ソフトウェアでシミュレーションシリーズがノーアイデアでもネタが尽きないと思っていたら、早々とネタ切れです。
循環参照以外のテクニックは何も使っていなかったということに気付かされました・・・
ということで、最近の「情報の科学」の教科書で定番化し始めている?ような気がする待ち行列のシミュレーションをしてみます。
いろいろな要素があるので、小分けにして取り上げていきたいと思います。
ある飲食店にお客さんが来て、何かを注文して食べるときに、どのくらい待ち時間が発生するかをシミュレーションしてみます。
見方を変えれば、CPUに仕事が来て、何か処理をする際に、どのくらい待ち時間が発生するかと読み替えても同じです。
今回は、お客さんが来る時間について考えることにします。
お客さんが来る確率分布って?
お客さんは気まぐれにやってきます。
仮に60秒に4人くらいと仮定しましょう。イメージはしょぼい学食を想定しています。(あくまでも架空の話ですよ)
60秒に4人ですが、15秒ごとにきっちり来てくれるわけではありません。
一定間隔で来たら、とっても楽なんですけどね・・・
で、調べました。
気が付くと毎度お世話になる統計Web のページです。ありがとうございます。
結論だけ使ってしまうと、どうやら指数分布です。
\(f(x)=\lambda e^{-\lambda x}\)が確率密度関数らしいです。
なぜ指数分布かを解釈しているページも見つかりました。
あえて誤解を恐れずざっくり言ってしまうと、お客さんが来たらそこで連続記録が途切れて、ゼロからやり直しになるから確率は単調減少しているという感じでしょうか。
で、\(f(x)=\lambda e^{-\lambda x}\)は確率密度関数なので、積分して\(x\)までに来店する確率という累積分布関数\(F(x)=1-e^{-\lambda x}\)を使って求める必要があります。
Excelでは、この累積分布関数は、=EXPON.DIST(x,lambda,TRUE) で求めることができます。
がんばって =1-EXP(-lambda*x) と書いてもよいです。
気を付けなければならないのは、この数式で求められるのは累積分布関数ということなんです。
0以上x以下の時間の範囲で来店する確率なんです。
Excelで来店する確率を表にしてみる
累積分布関数を使ってしまってよければ、これが累積確率です。
ということでそのまま表にしました。
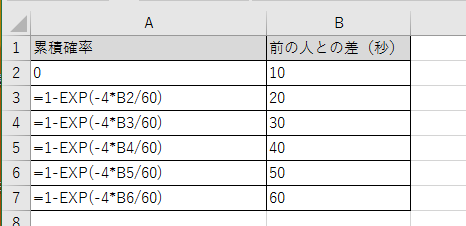
最初の値を0にして、一つずつずらすことによって、VLOOKUP関数で秒数に変換できます。
こんな離散的な秒数ではなく、連続した秒数で求めようとすると面倒なので、あきらめることにします。
これだと、別のことに応用しにくいので、確率がわかるようにします。
この値は累積なので、確率を求めるために差分を取ることにします。
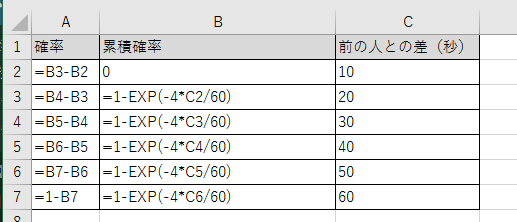
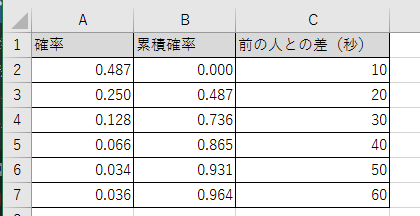
そうすると次のような値になります。
高校の授業ではどうするの?
結論から言います。確率分布の話は避けます。
数学で確率分布の説明を聞いている生徒は稀だろうということで、その説明に十分時間を取ることができないので避けます。
その結果、どうするか。ある程度、近似した値を与えて取りかかることにします。
生徒がアレンジするときに、指数分布が崩れたらどうするの? 気にしません!
結局、高校段階では数学Bで統計を学習しない限り、正規分布すらちゃんと学びません。
仕方ない・・・と割り切ることにします。
結果として、多少値を丸めて次のようにしてしまいます。
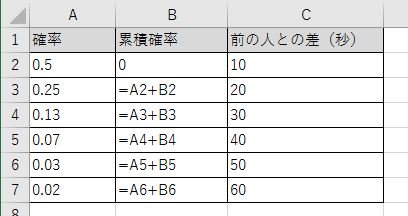
雰囲気だけかもしれないけれど指数分布に従っているかもしれないような気がする程度の確率分布に納まったという感じです。
今回はこれでおしまいにします。それではまた。
[mathjax]













ディスカッション
コメント一覧
まだ、コメントがありません