ブラックジャックでヒットすべき?スタンドすべき?(高校生が考えたモデル化とシミュレーション05)

こんにちは。乱数を使ったモデル化とシミュレーションの例を紹介します。
2016年の授業で,生徒がグループ活動で考えたアイデアを基に記事を書いています。
2016年はアメリカ大統領選挙の年で,オバマ大統領が2期8年務めた後任の大統領を決める選挙でした。
トランプ候補(後の大統領)とヒラリー・クリントン候補が激しく競り合っていたことから,トランプをシミュレーションしてみよう!となったようです。
で,比較的シミュレーションがしやすいと考えたのが,ブラックジャックだったようです。
ブラックジャックのかなりざっくりとしたルール
ディーラーとプレイヤーとで,カードの数字の合計が21に近くした方が勝ちというゲームです。
カードの数字をそのまま使わない例がいくつかあります。
- 絵札(J・Q・K)は10として扱う
- A(エース)は1または11として扱う
カードは最初,2枚配られます。
さらにカードを配ってもらうことも,そのままで勝負することもできます。
カードを1枚追加で配ってもらうことをヒット,現在の合計で勝負することをスタンドといいます。
ヒットした結果,21を超えてしまった場合をバーストといいます。
バーストになると即時で負けになってしまいます。
シミュレーションしてみよう
とにかく仮にヒットした場合にどうなるかをシミュレーションしてみます。
はじめにトランプをシャッフルする様子をシミュレーションしてみます。
ジョーカーを除く52枚のカードをシャッフルするには,52個の0以上1未満の乱数を発生させて順位を付けます。
厳密には52個の乱数が一致してしまう可能性が皆無ではないのですが,目を瞑ることにします。
これで,1から52までの整数がランダムな順番で発生します。
この値から1引くことで,0から51になり,13で割った商が0から3まで13個ずつになります。
この商をトランプのマークと対応付けることにします。
例えば,0…スペード,1…ハート,2…ダイヤ,3…クラブとしましょう。
13で割った余りに1足した値をトランプの数字とします。
1…A,11…J,12…Q,13…Kとします。
配ります。1枚目をプレーヤー,2枚目をディーラー,3枚目をプレーヤー,4枚目をディーラーにします。
計算のしやすさでは,交互にしない方がよいのですが,本当に配っている感じを出すためにこだわってみます。
5枚目のカードは,プレーヤーがヒットしたときに配られるカードになります。
Aが1でも11でもどちらにもできるので,Aが配られた枚数も調べておく必要があります。
ここまでの値を使って,はじめに配られた2枚のカードの合計と,ヒットしたときの3枚のカードの合計とをクロス集計してみます。
20000回ほどシミュレーションしてみました。
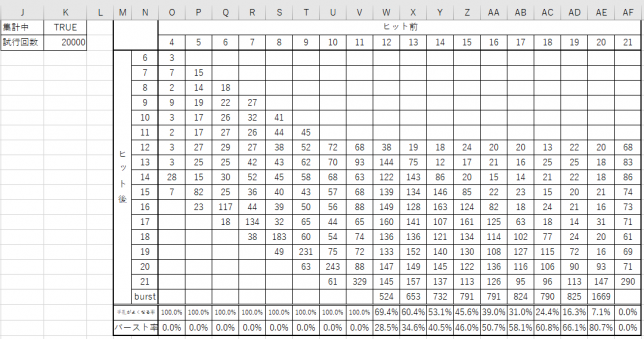
シミュレーションした結果から
上の表を見ながら,方針を考えてみます。
最初の2枚のカードの合計が11未満の場合には,ヒットしたときに絶対にバーストすることはないので,絶対にヒットします。
最初のカードの合計が12・13・14あたりでも,ヒットするとバーストしてしまう確率が案外高いようです。
10・J・Q・Kの4種類も10が加えられるカードがあるのは,大きな影響を与えます。
それでも,元の合計よりもヒットした方が値がよくなる確率も高いので,ヒットすることにしようと思います。
15のときには,値がよくなる確率よりもバーストする確率の方が高くなってしまいます。
バーストしないことが目的ではなく,ディーラーに勝つことが目的なので,とりあえずヒットすることにしてみます。
16・17あたりがスタンドする境目になるかと思います。
18~20のときは,合計がよくなる確率は低くなり,バーストする確率は高くなってしまうので,スタンドすることにします。
21の場合には,Aが含まれているのでバーストすることは絶対にありませんが,ブラックジャックになっているのを崩す必要はないので,スタンドです。
これで,とりあえず方針が決まりました。
今回はこれでおしまいにします。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません