高校でTF-IDF(2)

こんにちは。前回のTF-IDFの続きです。前回はTFについて整理しました。今回はIDFとTF-IDFをまとめていきます。
IDFとは
IDFは、Inverse Document Frequencyで、直訳してしまうと逆単語出現頻度といった感じでしょうか。まずはじめに定義式です。この定義式は一つに定まっておらず、書籍やサイトで調べると少しずつバリエーションがあります。授業では、
$${\rm idf}(t)=\log{\frac{N}{df(t)}}$$
を用いました。ここで
\(N\)は全文書数
\(df(t)\)は単語\(t\)が出現する文書数
です。書籍によってはこの式に\(+1\)して、すべての文書に出現する単語の値が\(0\)にならないようにしているものもあります。対数の底は任意と書かれた書籍がありましたので、授業では高校の数学で桁数を求めるのに常用対数を学習しており馴染みがあるだろうということで\(10\)を底とする常用対数を使いました。なお、この内容は、高校3年生を対象とした授業で行いました。
やはりこれではわかりにくいので、言葉を用いて次のように簡略化した表現に直します。
$$単語tの\rm{idf}=-\log{(全文書に対する単語tの出現率)}$$
としてしまうと、かなりわかりやすくなるのではないでしょうか。ここで\(\log\)の後ろの分数がなくなってしまったみたいですが、対数の性質の\(\log{\frac{a}{b}}=-\log{\frac{b}{a}}\)により分子と分母を入れ替えると±が入れ替わること、\(\frac{単語tが出現する文書数}{全文書数}\)を\(全文書数に対する単語tの出現率\)という表現にしたことで式を簡略化しています。これでもイメージしにくいと考え、\(全文書に対する単語tの出現率\)とIDFの関係を次のようなグラフで示しました。
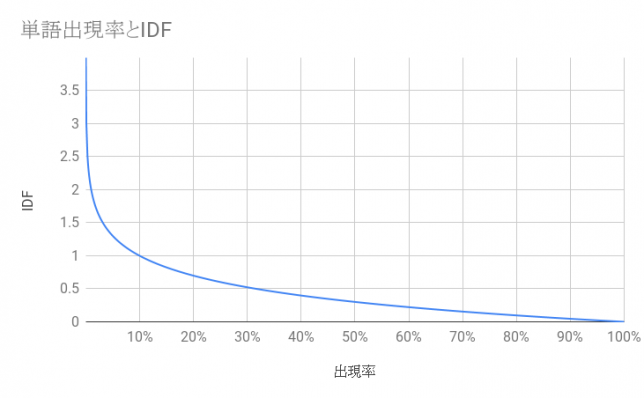
前回のTFは繰り返し何回も出てくる単語は値が大きくなるという特徴がありました。今回のIDFの特徴は次のようになります。
特定の文書について出現する単語は値が大きくなる
どの文書にも共通して出現する単語は値が小さくなる
球技を例にすると、「スリーポイントシュート」ならば「バスケットボール」、「ホームラン」といえば「野球」、「オフサイド」といえば「サッカー」とすぐに種目がイメージできる単語はIDFが高い傾向があります。逆に「ボール」といっても種目が特定できずIDFが低くなる傾向があります。「ラケット」は「サッカー」や「野球」ではなく、「テニス」や「卓球」のようなラケットを使う種目に限定され、IDFは中間的な値をとると考えられます。このような傾向を簡単に表現するために、「レア度」といった表現で説明してみました。
IDFを求めてみる
授業ではTFと同様にIDFの値を求めてみました。授業では、いちごの文章に登場する単語だけ求めましたが、時間の制約がないので出現語すべてのIDFを求めてみましょう。
例)次の文章に出現する単語のIDFを求めなさい。
いちごの文章:[ 果物 | ケーキ | ビタミン | ケーキ | 赤い ]
りんごの文章:[ 果物 | ジュース | 青森 | ビタミン | 赤い ]
キウィの文章:[ ビタミン | 毛 | 緑 | 黄色 ]
まず、全文書数は「いちご」・「りんご」・「キウィ」の3つになります。これが全文書数になります。
次に出現するすべての単語のIDFを求めてみましょう。
| 単語 | 出現する文書数 | IDF |
| 果物 | 2 | $$-\log{\frac{2}{3}}\approx 0.18$$ |
| ケーキ | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
| ビタミン | 3 | $$-\log{\frac{3}{3}}=0$$ |
| 赤い | 2 | $$-\log{\frac{2}{3}}\approx 0.18$$ |
| ジュース | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
| 青森 | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
| 毛 | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
| 緑 | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
| 黄色 | 1 | $$-\log{\frac{1}{3}}\approx 0.48$$ |
というようになります。果物でビタミンといえば特徴になりそうですが、この例で使った果物はいずれも「ビタミンC 多い 果物」での検索結果で見つけた果物なので、「ビタミン」という言葉は含まれていて当たり前のため、特徴とはならず、IDFの値は\(0\)になってしまっています。
TF-IDFを求めてみる
最後にTF-IDFを求めてみましょう。TF-IDFはTFとIDFの積です。つまり
$$\rm{tfidf}(t,d)=\rm{tf}(t,d)\times\rm{idf}(t)$$
です。それでは、IDFで用いた文章についてTF-IDFを求めてみましょう。
| 単語 | いちごのTF-IDF | りんごのTF-IDF | キウィのTF-IDF |
| 果物 | $$\frac{1}{5}\times(-\log{\frac{2}{3}})\approx 0.04$$ | $$\frac{1}{5}\times(-\log{\frac{2}{3}})\approx 0.04$$ | $$0\times(-\log{\frac{2}{3}})=0$$ |
| ケーキ | $$\frac{2}{5}\times(-\log{\frac{1}{3}})\approx 0.19$$ | $$0\times(-\log{\frac{1}{3}})=0$$ | $$0\times(-\log{\frac{1}{3}})=0$$ |
| ビタミン | $$\frac{1}{5}\times(-\log{\frac{3}{3}})=0$$ | $$\frac{1}{5}\times(-\log{\frac{3}{3}})=0$$ | $$\frac{1}{4}\times(-\log{\frac{3}{3}})=0$$ |
| 赤い | $$\frac{1}{5}\times(-\log{\frac{2}{3}})\approx 0.04$$ | $$\frac{1}{5}\times(-\log{\frac{2}{3}})\approx 0.04$$ | $$0\times(-\log{\frac{2}{3}})=0$$ |
| ジュース | $$0\times(-\log{\frac{1}{3}})=0$$ | $$\frac{1}{5}\times(-\log{\frac{1}{3}})\approx 0.10$$ | $$0\times(-\log{\frac{1}{3}})=0$$ |
| 青森 | $$0\times(-\log{\frac{1}{3}})=0$$ | $$\frac{1}{5}\times(-\log{\frac{1}{3}})\approx 0.10$$ | $$0\times(-\log{\frac{1}{3}})=0$$ |
| 毛 | $$0\times(-\log{\frac{1}{3}})=0$$ | $$0\times(-\log{\frac{1}{3}})=0$$ | $$\frac{1}{4}\times(-\log{\frac{1}{3}})\approx 0.12$$ |
| 緑 | $$0\times(-\log{\frac{1}{3}})=0$$ | $$0\times(-\log{\frac{1}{3}})=0$$ | $$\frac{1}{4}\times(-\log{\frac{1}{3}})\approx 0.12$$ |
| 黄色 | $$0\times(-\log{\frac{1}{3}})=0$$ | $$0\times(-\log{\frac{1}{3}})=0$$ | $$\frac{1}{4}\times(-\log{\frac{1}{3}})\approx 0.12$$ |
計算結果をもとに特徴語を抽出できます。TF-IDFが大きい方が特徴ごと考えられます。しかし、単にTF-IDFが高いから特徴語としてしまうと「~することができる。」というような文から得られる形態素「する」「こと」「できる」という語のTF-IDFがそれなりに高い値になってしまいます。このように不要と考えられる単語をストップワードとして計算前に除外してしまうか、計算後に特徴語を抽出する際に意味を考えて選択するかということになります。授業では、計算後に意味を取りながら不要な単語はないものとして除去することを使いました。今にして思えばプログラムは数行しか違わないので、ストップワードを先に除去した方がストップワードを含まない値にならないので良かったと思います。
ここまでは、数値での計算を行ってきましたが、数値で表現された表は案外読みにくいものです。次回はビジュアル的な表現について整理したいと思います。それではまた。











ディスカッション
コメント一覧
まだ、コメントがありません