情報科の目で見る数学科学習指導要領(7)ハノイの塔

こんにちは。まだまだ数学シリーズが続きます。今回は「ハノイの塔」です。
学習指導要領解説では
次期学習指導要領では、「数列」と「ベクトル」が別々の科目(というよりも、今までこの2つが一緒だった理由はよくわかりませんが・・・)ということが、数学Bで話題になっていますが、「数学B」でも日常の事象や社会の事象に注目することになっています。
漸化式について理解し,事象の変化を漸化式で表したり,簡単な漸化式で表された数列の一般項を求めたりするとともに,事象の再帰的な関係に着目し,日常の事象や社会の事象などを数学的に捉え,数列の考えを問題解決に活用すること(ア(ウ),イ(イ))
事象の再帰的な関係に着目し,その関係を漸化式で表現することを通して,漸化式の意味を理解できるようにする。また,簡単な漸化式を用いて表された数列の一般項を求めることができるようにする。ここでいう簡単な漸化式とは,一次の形の隣接二項間の漸化式のことである。指導に当たっては,具体的な事象を取り上げ,その事象における再帰的な関係を漸化式で表すことを通して,漸化式の有用性や一般項を求める意味を理解できるようにすることが大切である。例えば,「ハノイの塔」や「複利計算」などを取り扱うことが考えられる。指導に当たっては,場面に応じて,コンピュータなどの情報機器を用いるなどしてその変化の様子を調べ,一般項を予想したり,導き出した一般項の妥当性を検証したりすることも大切にする。このような活動を通して,数列の考えを問題解決に活用する力を養うようにする。
漸化式の考え方は、改めて書く必要がないくらい、プログラミングでの再帰と密接な関係にあります。数学では「ドミノ倒し」で例えられることが多いと思います。最初のドミノが倒れると、次のドミノが倒れ、それによりさらに次のドミノが倒れ、それによりさらにさらにその次のドミノが倒れ、・・・とずっと倒れ続けていきます。それと同じように、初項が決まると、初項が決まることにより第2項が決まり、第2項が決まることにより第3項が決まり、・・・と続けて項の値が決まっていくというイメージです。例えば
\[\begin{cases} a_{1} = 5 \\ a_{n+1} = 2a_{n} + 3 & ( n \geq 1 ) \end{cases}\]
で、\(a_{2}=2 \times 5 + 3=13\),\(a_{3}=2 \times 13 + 3=29\),・・・という感じで、前の項を使って次の項を作っていくものです。
プログラミングでの再帰は似たような感じですが、マトリョーシカを取り出す手順のような感じです。大きいマトリョーシカを開けて小さいマトリョーシカを取り出し、ちょっと小さいマトリョーシカを開けてさらに小さいマトリョーシカを取り出し、さらに小さいマトリョーシカを開けてもっと小さいマトリョーシカを取り出し、・・・一番小さいマトリョーシカを取り出したら1つ大きいマトリョーシカを組み立て、その外側のマトリョーシカを組み立て、・・・、一番大きいマトリョーシカを組み立てると、全部のマトリョーシカが勢ぞろいします。再帰は、1つずつサイズダウンしていき、一番小さいものは特別な操作をするという感じでしょうか。
再帰の考え方を「ハノイの塔」を題材に考えてみます。
ハノイの塔とは
ハノイの塔はパズルの一種です。次のルールで円盤を動かしていきます。
- 3本の杭が並んで立っている
- すべて大きさが違う複数の穴が開いた円盤がある
- 上にいくほど小さい円盤になるようにして、左端の杭にくし刺しになって積み重なっている
- 1回の手順で1枚の円盤を別の杭に移動できる。このとき、小さい円盤の上には、それより大きい円盤を乗せることはできない
- すべての円盤を隣の杭に移すことができれば完成
というものです。図で表すと
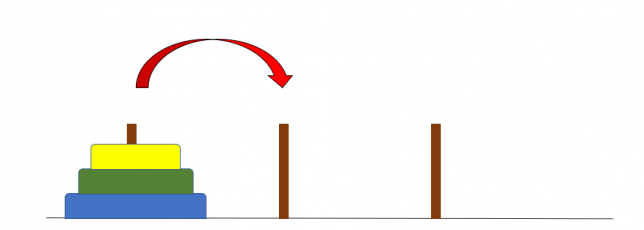
ということが目標です。
完成形を作るためには、次のように考えるとうまくいきます。
まず、1番小さい円盤からn-1枚目までの円盤は、一番大きい円盤を動かす邪魔をしているので右端に逃がしておきます。
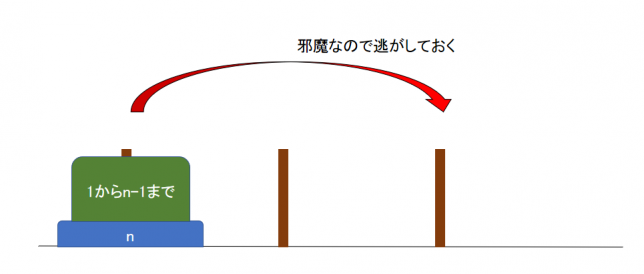
次に、一番大きいn枚目の円盤を隣の杭に動かします。
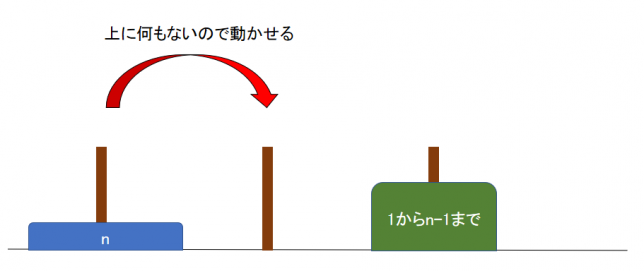
そして、逃がしておいたn-1枚の円盤を、一番大きい円盤の上に動かします。
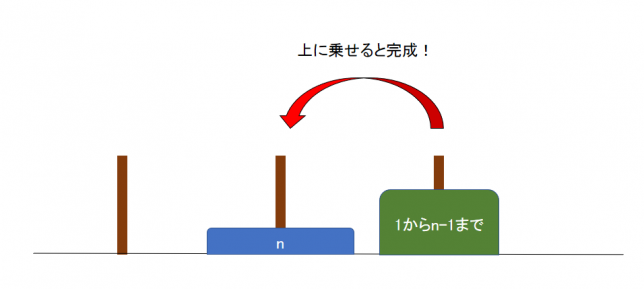
これで完成形ができます。漸化式で移動回数を求めると次のようになります。\(a_{n}\)は、n枚の円盤を動かす回数です。\(a_{n-1}\)を使って表すと、\(a_{n} = a_{n-1} + 1 + a_{n-1}\)になります。また、一番小さい円盤は、上に乗っている円盤はないので\(a_{1}=1\)になります。これをまとめて漸化式を作ると
\[\begin{cases} a_{1} = 1 \\ a_{n+1} = 2a_{n} + 1 & ( n \geq 1 ) \end{cases}\]
このように立式できれば、隣接2項間の漸化式になります。一般項を求めるのは数学で定番の問題です。
再帰を用いたプログラム
次にプログラムを使って、動かし方を表示してみましょう。移動元frからn-1枚をuseに避けておき、n番目の円盤を移動元frから移動先toに動かし、避けておいたn-1枚をuseからtoに動かす手順により完成形を作ることができます。Pythonのプログラムは次になります。
def hanoi( n, fr, to, use ):
if n == 1:
print( '円盤 1 : ' + fr + ' → ' + to )
return
hanoi( n-1, fr, use, to )
print( '円盤 ' + str(n) + ' : ' + fr + ' → ' + to )
hanoi( n-1, use, to, fr )
hanoi( 5, 'A', 'B', 'C' )
5枚の円盤を動かした場合の移動方法を載せます。
円盤 1 : A → B
円盤 2 : A → C
円盤 1 : B → C
円盤 3 : A → B
円盤 1 : C → A
円盤 2 : C → B
円盤 1 : A → B
円盤 4 : A → C
円盤 1 : B → C
円盤 2 : B → A
円盤 1 : C → A
円盤 3 : B → C
円盤 1 : A → B
円盤 2 : A → C
円盤 1 : B → C
円盤 5 : A → B
円盤 1 : C → A
円盤 2 : C → B
円盤 1 : A → B
円盤 3 : C → A
円盤 1 : B → C
円盤 2 : B → A
円盤 1 : C → A
円盤 4 : C → B
円盤 1 : A → B
円盤 2 : A → C
円盤 1 : B → C
円盤 3 : A → B
円盤 1 : C → A
円盤 2 : C → B
円盤 1 : A → B
再帰を用いないプログラム
再帰を使って考えると単純になります。そのため、再帰は多くの場面で使われます。しかし、一回り小さいサイズとの関係を考えるのは、慣れないと難しいかもしれません。そのため、比較のために再帰を使わないプログラムで書いてみます。
上の結果をみると、円盤1は1回おきに移動します。また、円盤1の動きは「A→B→C→A→B→・・・・」と循環しています。これは、いろいろな値に変えて調べると、円盤の枚数が奇数の場合は「A→B→C→A→B→・・・・」の向きで、円盤の枚数が偶数の場合は「A→C→B→A→C→・・・・」と回り方が変わります。
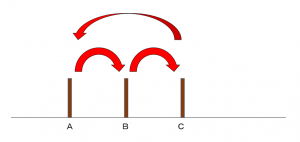
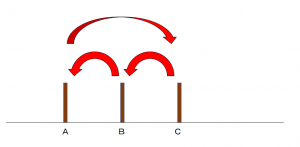
回る方向をdirection変数にしました。nが奇数のときは+1、nが偶数のときは-1になります。これによりmove1,move2,move3は奇数ではA,B,C、偶数ではA,C,Bとなります。これにより移動している部分は、プログラムでの32行目から39行目です。move1が円盤1がある杭、move2が次の移動先の杭です。
stateは円盤がどのように置かれているかを示す変数です。キーは杭の名前(左から順にA,B,C)で、バリューは円盤が積み重なっている様子をリストを用いて表現しています。リストにn+1の要素を入れているのは、リストが空になると一番上にある円盤の大きさを比較している23行目でエラーになってしまうためです。n+1は他の円盤より大きいので、番兵の役割を果たします。
円盤1が動かないときは、他の杭の一番上の円盤どうしを比較すると必然的に移動できる円盤は決まります。下のプログラムでは23~30行では、popで移動する円盤を取り出し、appendで円盤の上に乗せています。この操作をAとCの杭が番兵だけになるまで繰り返します。これで再帰版と同じ動作をするプログラムになります。
n = 5
move = [ 'A', 'B', 'C' ]
direction = (n % 2) * 2 - 1
move1 = move[0]
move2 = move[ direction % 3 ]
move3 = move[ direction*2 % 3 ]
state = { 'A':list(range(n+1,0,-1)) , 'B':[n+1] , 'C':[n+1] }
disk = state[move1].pop()
state[move2].append(disk)
print( '円盤 1 : ' + move1 + ' → ' + move2 )
tmp = move1
move1 = move2
move2 = move3
move3 = tmp
while( len(state['A'])>1 or len(state['C'])>1 ):
if state[move2][-1]<state[move3][-1]:
disk = state[move2].pop()
state[move3].append(disk)
print( '円盤 ' + str(disk) + ' : ' + move2 + ' → ' + move3 )
else:
disk = state[move3].pop()
state[move2].append(disk)
print( '円盤 ' + str(disk) + ' : ' + move3 + ' → ' + move2 )
disk = state[move1].pop()
state[move2].append(disk)
print( '円盤 1 : ' + move1 + ' → ' + move2 )
tmp = move1
move1 = move2
move2 = move3
move3 = tmp
結果は同じになるので省略します。今回はこれでおしまい。それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません