度数分布表とヒストグラムを作ってみる

こんにちは。今回は度数分布表とヒストグラムを作ってみます。
以下の説明は概略がわかる程度に書いていますので、不正確な部分があれば訂正しますので教えていただけると助かります。
度数分布表とは
前回まで取り上げたドットプロットは、データに対応するように数直線上にドットをプロットするものでした。
数直線を一定区間ごとに区切り、その区間に含まれるデータの個数を表にまとめたものを度数分布表といいます。
区間のことを階級、データの個数を度数といいます。
また、階級の端点の平均値を階級値といいます。
度数分布表は次のような表になります。
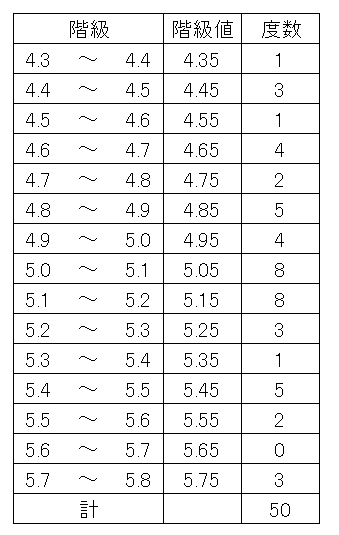
ヒストグラムをPython + matplotlib で描いてみる
それでは、プログラムでヒストグラムを描いてみます。
一応、念のためですが、棒グラフとの違いは、横軸が連続した値になっていることです。
ヒストグラムは柱状グラフともよばれています。
import seaborn
import matplotlib.pyplot
iris = seaborn.load_dataset( 'iris' )
df = iris[ iris['species']=='setosa' ]
ret = matplotlib.pyplot.hist( df['sepal_length'], bins=15 )
matplotlib.pyplot.show()
print( '階級 , 階級値 , 度数' )
for i, num in enumerate( ret[0] ):
midpoint = ( ret[1][i] + ret[1][i+1] ) / 2
print( '{0} - {1} , {2} , {3}'
.format( ret[1][i], ret[1][i+1], midpoint, ret[0][i] ) )
データは前回と同じirisですが、setosaの品種だけを取り出してヒストグラムを描きたかったので、そのためだけに seabornをインポートしています。
単にデータを取り出すのなら、seabornのデータの方が楽そうな気がします。
ヒストグラムは、次のようになります。
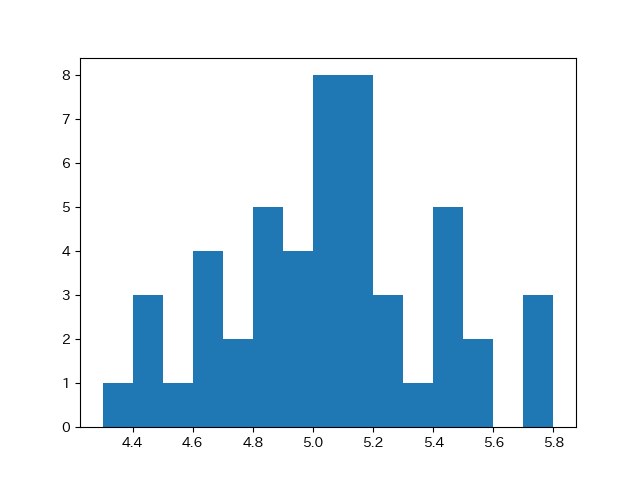
プログラムでは、ついでに度数分布表として使えるテキストも出力しています。
その結果です。
階級 , 階級値 , 度数
4.3 - 4.3999999999999995 , 4.35 , 1.0
4.3999999999999995 - 4.5 , 4.449999999999999 , 3.0
4.5 - 4.6 , 4.55 , 1.0
4.6 - 4.7 , 4.65 , 4.0
4.7 - 4.8 , 4.75 , 2.0
4.8 - 4.9 , 4.85 , 5.0
4.9 - 5.0 , 4.95 , 4.0
5.0 - 5.1 , 5.05 , 8.0
5.1 - 5.2 , 5.15 , 8.0
5.2 - 5.3 , 5.25 , 3.0
5.3 - 5.4 , 5.35 , 1.0
5.4 - 5.5 , 5.45 , 5.0
5.5 - 5.6 , 5.55 , 2.0
5.6 - 5.7 , 5.65 , 0.0
5.7 - 5.8 , 5.75 , 3.0
階級の桁数が一部多くなっているのは浮動小数点数の丸め誤差の影響なんでしょうか?
とりあえず、気にしないことにします。
階級幅の問題
ヒストグラムは階級幅を変えることにより、(よいかどうかは別にして)データの見せ方を変えることができます。
プログラム中の bins=15 の数値を変えてみます。
bins = 5 とした場合のヒストグラムです。
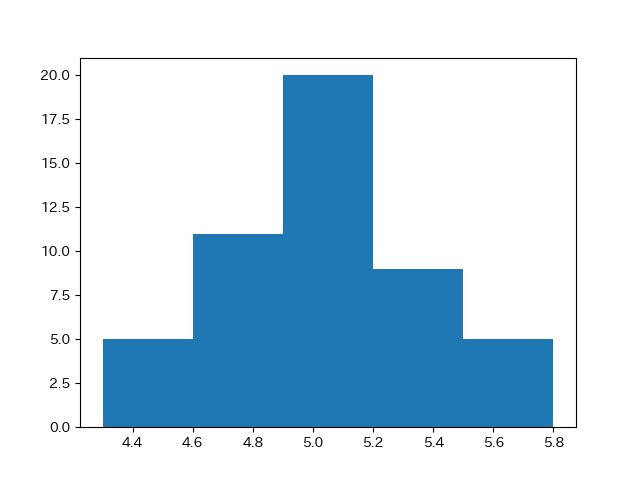
bins = 3 とした場合のヒストグラムです。
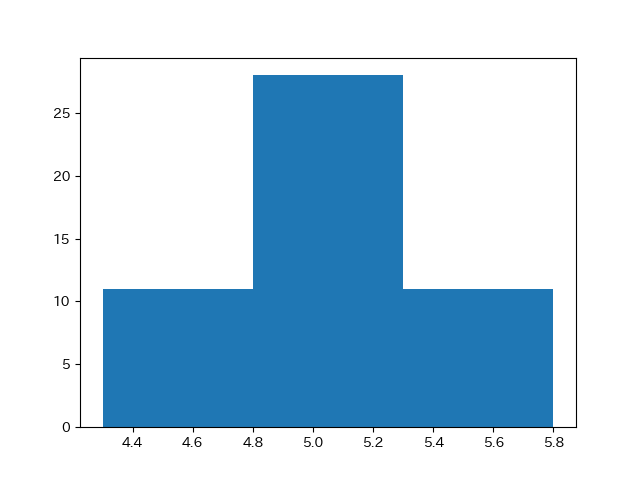
bins = 1 とした場合のヒストグラムです。
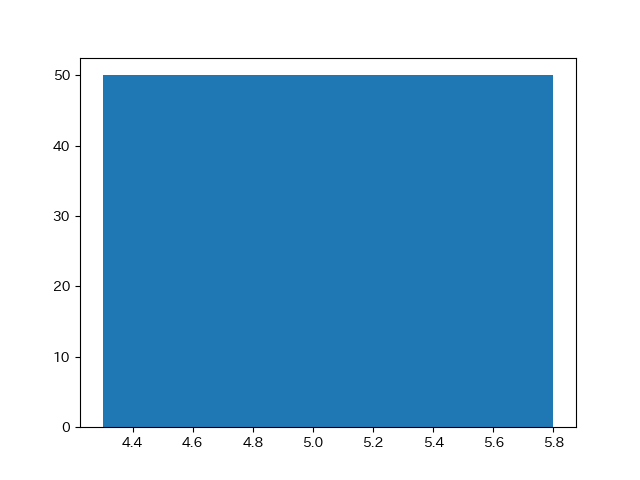
もうこれはヒストグラムとはよべない代物になってしまいました。
これは極端な例なのでわかりやすいのですが、微調整すれば分布の印象を変えることができてしまいます。
階級数を決める目安として、スタージェスの公式というものがあるようです。
データの個数を\(N\)とするとき、
\[k=1+\log_2{N}\]
により求まる\(k\)が階級数の目安というようです。
今回は\(N=50\)なので、\( k=1+log_2{50} ≒ 6.64 \)というなります。
それでは、 bins=7としてヒストグラムを描いてみます。
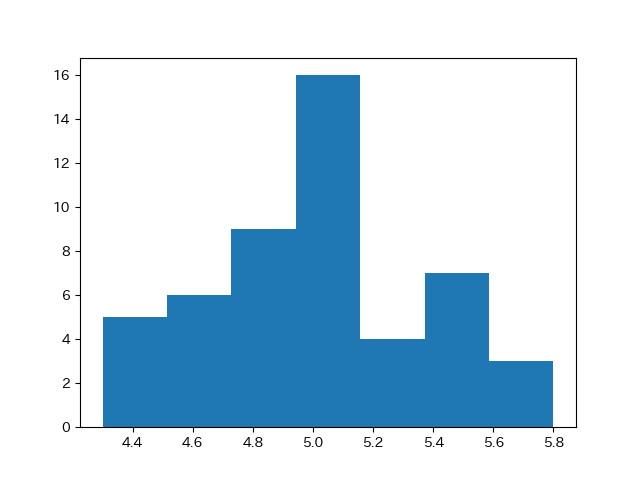
ヒストグラムを R で描いてみる
次に、Rを使ってヒストグラムを描いてみます。
setosa <- subset( iris, Species=='setosa' )
hist( setosa$Sepal.Length )
このプログラムで、次のようなヒストグラムが描けます。
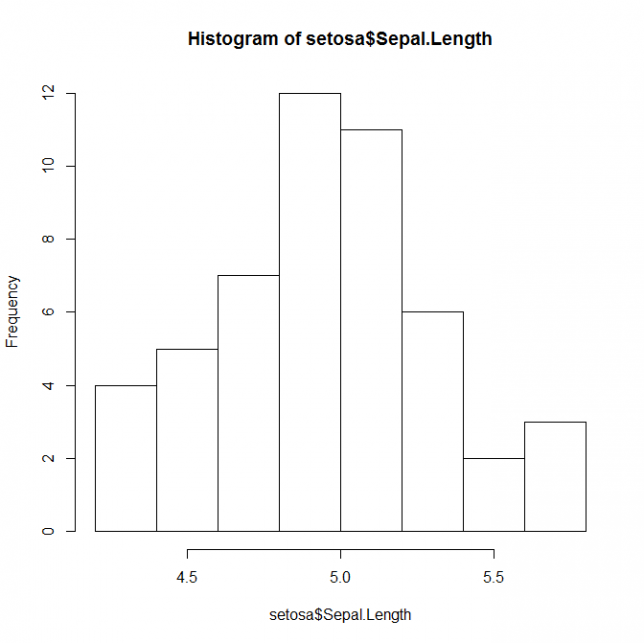
breaksに値を与えて、階級を変えてみます。
setosa <- subset( iris, Species=='setosa' )
hist( setosa$Sepal.Length, breaks='Scott' )
このように変わります。
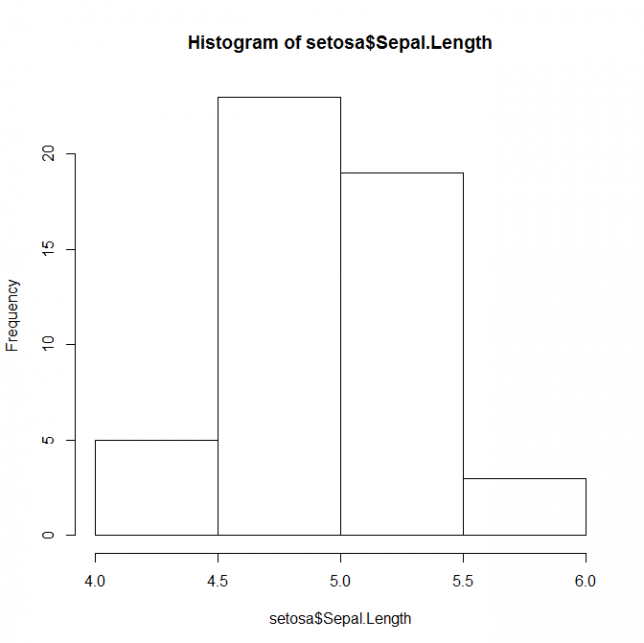
階級の数を breaks=3 と直接指定してみます。ついでに、col=’orange’で色を付けてみます。
setosa <- subset( iris, Species=='setosa' )
hist( setosa$Sepal.Length, breaks=4, col='orange' )
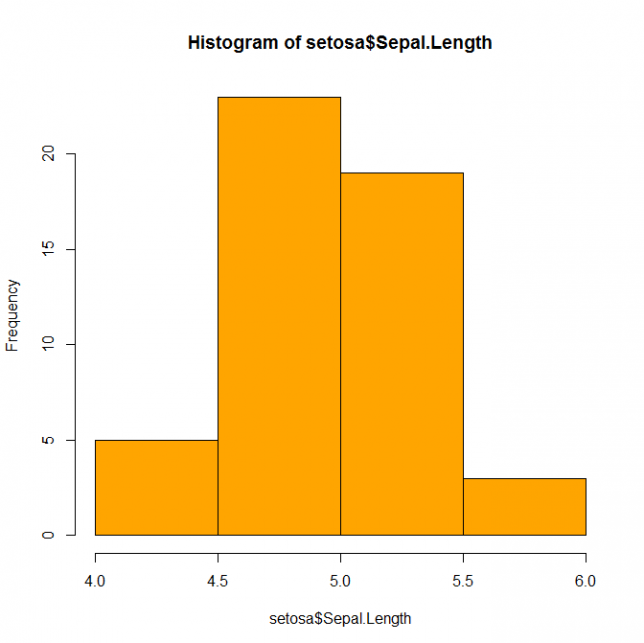
目的がグラフのパラメーターを網羅することではなく、一通りのグラフをほぼ最小限のプログラムで描いてみるということなので、今回はこれでおしまいにします。それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません