席替えのシミュレーション あの席をただ一つねらっているんだよ(高校生が考えたモデル化とシミュレーション03)

こんにちは。久しぶりの高校生が考えたモデル化とシミュレーションシリーズです。このシリーズは、生徒が授業でやったままではなく、生徒のアイデアをもとに再構成していることをご了承いただければと思います。
席替えのモデルを作ろう
今回の題材は『席替え』ということで、古いのですが、学園天国の出だしの歌詞のようなタイトルとしました。
席替えネタはいくつかバリエーションがあります。今回は、「あの人と隣の席になりたい!」という想いをコンピュータ上で実現していきます。
モデル化をする前に次にように決めます。
- クラスの人数は41人(勤務校では、ありがちな人数です。)
- 座席はくじ引きで決める。黒板が見えないから優先的に前の方に座るといったことは考えない
- 座席の配置は横6列、縦7行(教室の入口に近い列は、縦6行で一番後ろの席がない)
- 隣の席とは、隣の列の前から数えて同じ位置に座ることとする
といったあたりということにしておきましょう。
座席に番号を付けるには
それでは、次に座席番号を付けていきます。普通は1から順に数えていくので、次のようになるのではないでしょうか。
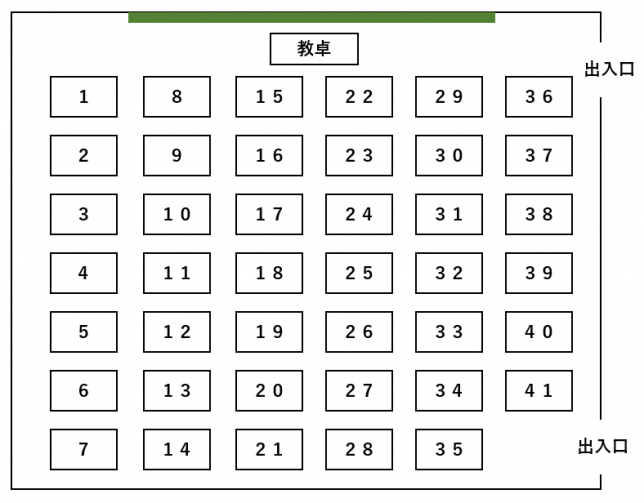
今回の目的としては、両隣のいずれかに座ることを考えるだけなので、自分の席±7の位置に「ねらっているあの人」の席があれば大丈夫です。
ちなみに、出入口側から1、2、・・・と番号を付けた場合は、自分とあの人のいずれかが出入口に一番近い列になったときには単純に調べられなくなることに注意です。
これで座席の番号を決定してもよいのですが、より複雑なことを考えるときには、工夫しておいた方が扱いやすくなるので、その方法についても紹介しておきます。
上の座席表で、横方向のどの列にいるかを調べるときに、実は面倒になります。下の図のように、0から番号を付けておくと簡単に調べられます。
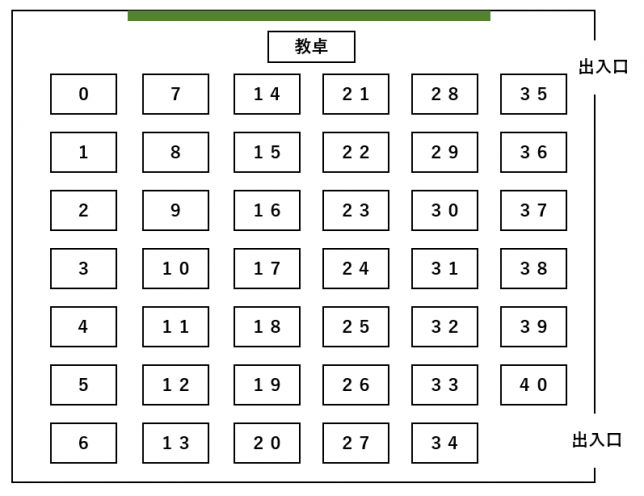
大した違いはなさそうですが、実は大きく違います。
座席番号を、縦方向の席の数7で割ると、左端の列の商はすべて0、左から2列目の商はすべて1、・・・と商を求めることにより簡単に求めることができます。
また、前からの位置についても、縦方向の席の数7で割った余りを使って考えられます。一番前の行は余りが0、前から2番目の行は余りが1、・・・と同じ余りになることを使うことができます。
規則性があるものを扱うテクニック(というほどではないですが・・・)の一つに、商と余りを使うことが挙げられます。
シミュレーションによって何を求めるの?
シミュレーションをして、「やった!隣になれた!」、「あぁ・・残念。離れちゃった・・・」と画面を見ながら一喜一憂していても、飽きるし、数回見たら「そんなもんか」という感じておしまいになるし、有用な使い方にはなりません。
ここでは、2つのことを考えることにします。
一つは「隣になる確率」を求めます。
もう一つは、何回席替えをすれば隣になれるのかという、「はじめて隣になるまでの席替え回数の期待値」を求めます。
このように、何を求めるかという観点を決めないと、問題を発見したり、問題を解決したりということにつながりません。
案外、自分自身で問題意識をもってシミュレーションをするということは難しいかもしれません。
それでは、まずは席替えをするための数式モデルとシミュレーションを始めることにします。
席替えシミュレーション by Excel
席替えをしましょう。そのための数式モデルは次になります。
- 乱数 = rand()
- 座席番号 = rank(乱数,全員分の乱数) – 1
- 横の位置 = int(座席番号 / 7)
- 縦の位置 = mod(座席番号, 7)
- 隣かどうかの判定 = and( 自分の縦の位置=あの人の縦の位置, abs(自分の横の位置-あの人の横の位置)=1 )
により、隣かどうかの判定ができます。それでは、Let’s Excel!
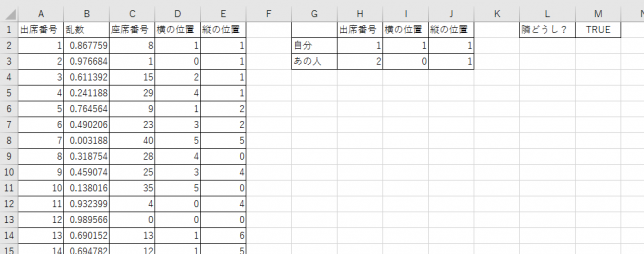
上の数式モデルに加えて、自分とあの人の出席番号を選ぶことができるよう、若干変えましたが、上の画面のようにシミュレーションできます。
乱数とrankを使っているのは、座席番号が同じになってしまうのを避けるためです。rand()は0以上1未満の小数で乱数を発生するので、重複することが稀であると考えられるからです。席替えをして、同じ座席番号が出たら、一人が椅子に座って、もう一人がその人の膝の上に座るということは避けたいからです。
隣どうしになる確率は?
それでは、確率を求めてみましょう。とりあえず1000回試行してみます。
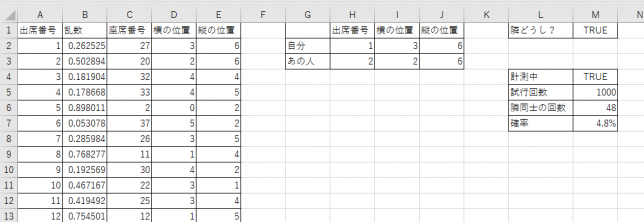
L・M列に計測するための表を追加しました。試行回数・隣同士の回数は、循環参照を使えば数えることができます。
乱数の出方によりますが、1000回中48回隣同士になったので、頻度をもとに考えると4.8%程度となります。多いのかな・・・?少ないのかな・・・?
何回席替えをすれば隣どうしになれるの?
次は、席替えを何回すればあの人と隣どうしになれるかを考えます。
隣どうしになるまで席替えを繰り返し、そのときの回数を調べます。1回だけだと偶然になるので、500回隣の席になるまで回数を調べて、平均を求めることにします。
高校では、期待値が数学Bに移ってしまいました。数学Bでは、多くの高校では「数列」・「ベクトル」をやっているので存在感がありませんが、本当は重要な概念だと思います。数学Aの確率に含めた方がよかったんじゃないかな。
それではシミュレーションをしてみましょう。
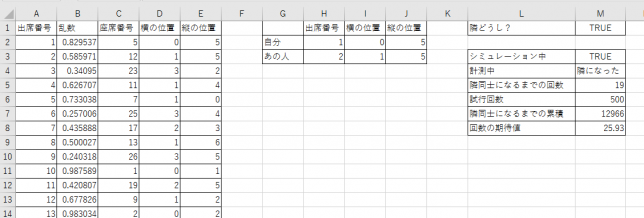
きれいに書くことができませんでしたが、一応シミュレーションできました。
なんと、あの人と隣の席になるためには、平均して25.93回も席替えをする必要があるという衝撃の予測が出ました!!!
だいたい年間の登校日数は200日程度なので、3~4日ごとに席替えをすることで、気になるあの人と隣どうしになれることが推測できました。
どうしても隣どうしになりたい人は、担任の先生に3~4日ごとに席替えをするようにお願いしてみてください。たぶん却下されるでしょうけど・・・
一応、Excelのファイルを載せておきます。
今回はこれでおしまいにします。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません