表計算ソフトウェアでシミュレーション(8)待ち行列のシミュレーション⑤窓口を3個にしてみる

こんにちは。まだまだ待ち行列を続けます。
窓口が2個で待ち時間が減るのなら、さらにもう1個増やして3個にすれば、待ち時間が減るんじゃね?というノリで窓口3個バージョンを作ってみます。
先に完成形を確認しましょう
どのような表を作るか先に見ておくと見通しが立ちます。
ということで、スクリーンショットを載せます。
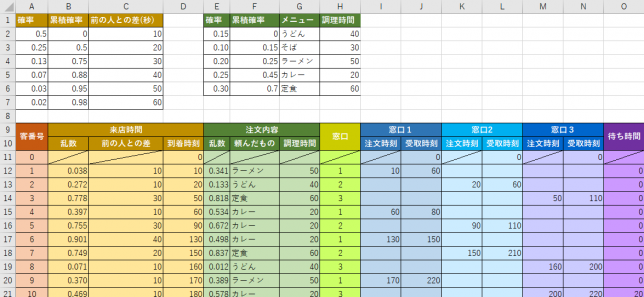
どの窓口に並ぶかを決める
まず、お客さんの並び方を決めます。
前回の窓口2個と同じように1列で並び、空いた窓口に進む方式にします。
(コンビニ方式ですよ!誰ですか?トイレ方式なんて言っているのは!)
前の人までの各窓口の終了時間を調べて、一番早く空く窓口がどこかを調べます。
窓口1では、次の式で求められます。
MAX(0人目の受取時刻:前の人までで最後に窓口1に並んだ人の受取時刻)
0人目は初期値を与えるためのダミーデータなので時刻は0ですが、絶対参照を使うと数式モデルがすっきりするのでうまく使った方がよいです。
窓口2,3についても同じです。
このうち、一番早く受け取り終わった窓口に行けばよいので、次のような数式モデルを作ることができます。
3つの窓口で一番最初に空く時刻を次の式で調べます。
MIN(前の人までで最後に窓口1に並んだ人の受取時刻,前の人までで最後に窓口2に並んだ人の受取時刻,前の人までで最後に窓口3に並んだ人の受取時刻 )
この時刻をもとに、どの窓口に並ぶかを決めます。
=IF(3つの窓口で一番最初に空く時刻=窓口1が空く時刻,1,IF(3つの窓口で一番最初に空く時刻=窓口2が空く時刻,2,3))
表計算ソフトウェアの数式をそのまま載せるとすごいことになりますが、一応載せておきます。
=IF(MIN(MAX($J$11:J11),MAX($L$11:L11),MAX($N$11:N11))=MAX($J$11:J11),1,
IF(MIN(MAX($J$11:J11),MAX($L$11:L11),MAX($N$11:N11))=MAX($L$11:L11),2,3))
窓口3の注文時刻と受取時刻を求める数式モデルは、窓口2とほぼ同じなので省きます。
待ち時間を求める式
どの窓口に並ぶかがさまざまなタイミングによって変わるので、注文時刻と受取時刻が表示される場所が変わってしまいます。
IF関数で場合分けしてもよいのですが、ひそかに窓口をもっと増やすことを企んでいるので、あっさり書きたいところです。(上の式はあれでいいのか・・・?)
そこで、MAX関数を使います。そうすると、空白は無視して最大の数値を拾ってくれます。
それにより次のような式で待ち時間を求めることができます。
=MAX(窓口1の注文時刻, 窓口2の注文時刻, 窓口3の注文時刻) – 到着時刻
これで、待ち行列をシミュレーションする部分はおしまいです。
時刻の平均値を求める
それでは、到着時刻、注文時刻、受取時刻、待ち時間について店にやってきた順番ごとに平均値を求めてみます。
数式については、ここまでの方法で求められるので省きます。
平均値を求める部分のスクリーンショットを載せます。
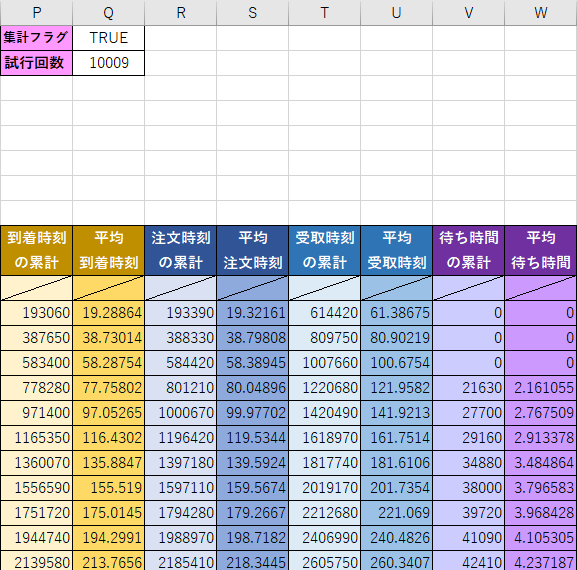
微妙に1万回を超えてしまいました。
これまでの値と比較してみましょう。
5人目のお客さんの数値を左から順に窓口1個、窓口2個、窓口3個になっています。
平均到着時刻 ・・・ 97.158秒 → 97.564秒 → 97.052秒
平均注文時刻 ・・・ 189.289秒 → 113.086秒 → 99.977秒
平均待ち時間 ・・・ 92.131秒 → 15.522秒 → 2.768秒
(平均受取時刻 ・・・ 231.314秒 → 155.050秒 → 141.921秒)
待ち時間3秒というのは誤差の範囲です。
ちなみに20人目のお客さんでは、待ち時間が
430.21秒 → 56.72秒 → 4.68秒
と、待ったといえるかどうかの時間まで短縮されました。
視覚化してみる
行列の様子を視覚化してみました。

ちなみにAA12のセルに入っている数式は次になります。
=IF(AND($D12<=AA$10,AA$10<MAX($I12,$K12,$M12)),"待", IF(AND(MAX($I12,$K12,$M12)<=AA$10,AA$10<MAX($J12,$L12,$N12)),"窓", “"))
今回はこれでおしまいにします。それではまた。













ディスカッション
コメント一覧
まだ、コメントがありません