表計算ソフトウェアでシミュレーション（９）待ち行列のシミュレーション⑥窓口ごとに並ぶ（２つの窓口）
こんにちは。まだまだ待ち行列を取り上げます。
並び方を変える
前回までは１列に並んで空いた窓口に並ぶ方式で、待ち行列の様子をシミュレーションしました。
ところがスーパーでは、レジごとに並んでいます。
列が短いと思って並んでみたら、なぜか前の人がもたついてしまって、結果として別のレジに並べばよかったと後悔することは少なくありません。
このようなスーパーのレジでの並び方と同じ並び方をシミュレーションしてみます。
窓口ごとに並んでいる人数を調べます。
このとき、料理を作ってもらっている人がいる窓口に並んだ場合には待つことになるので、ある時刻でのその人も含めた行列の長さを次のように調べます。
＝到着後に窓口１に並んだ人の人数ー窓口１ですでに料理を受け取った人の人数
窓口２でも同様に行列の長さを求めることができます。
表計算ソフトウェアに入力する数式は次のようになります。
=COUNTIF($I$11:$I11,"<“&D12)-COUNTIF($K$11:$K11,"<="&D12)
ちなみに、表は次のようになっています。
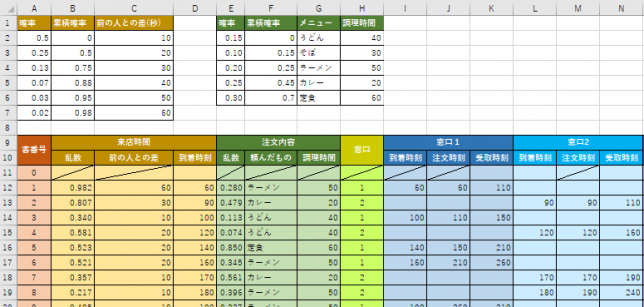
どちらの列に並ぶかは、次で決められます。
=IF(窓口１に並んだ人数<=窓口2に並んだ人数,1,2）
先ほどの数式とあわせると、表計算ソフトウェアでの数式は次になります。
=IF(COUNTIF($I$11:$I11,"<“&D12)-COUNTIF($K$11:$K11,"<="&D12)<=COUNTIF($L$11:$L11,"<“&D12)-COUNTIF($N$11:$N11,"<="&D12),1,2)
並び方を変えた結果
５０００回ほどシミュレーションして、同じ窓口２個の場合と比較してみます。
シミュレーションで最も差が大きくなる最後のお客さん（２０人目）で比較してみます。
１列に並んで空いた窓口に進む方式（トイレ方式） ・・・ 待ち時間 ５６．７３秒
２つの窓口に、窓口ごとに並ぶ方式（スーパー方式）・・・ 待ち時間 ６１．１０秒
優位な差といえるかどうかの検証は必要ですが、１列に並んで空いた窓口に進む方式（トイレ方式）のほうが若干待ち時間が短いといえそうです。
今回はこれでおしまいにします。それではまた。