数式の構文解析木を作る前に
こんにちは。
前回、字句解析器を作ったので、ちゃんと計算できるようにします。
そのためには、数式の構文を解析しなければなりません。
そもそも、数式はどのような構成になっているのでしょうか。
四則演算がある、括弧が使える・・・など漠然としていることを整理する必要があります。
また、かけ算とわり算は、たし算と引き算よりも優先順位が高いといったことも考えなければなりません。
このようなことを考えながら数式を構文解析する方法を考えていきます。
数式の構成要素
数式とはなんでしょうか？
というのは哲学的な問いではなく、単に分解していくだけです。
数式を分解する
中学校の数学で、単項式と多項式について学習します。
一般の数式は単項式を足したり引いたりすることで作られる多項式です。
中学校の数学では、文字式を対象に単項式や多項式という表現を使っていますが、数値だけの場合も同じように考えることにしましょう。
ここでは、表記の方法については割愛しますが、バッカス・ナウア記法(BNF)では次のように表現できます。
<expression>::=<term><operator2><term> | <term>
ここで、<term> は項、<operator2> はプラス（＋）またはマイナス（ー）の演算子になります。
なお、レールロードダイアグラムという方法で記述すると次になります。
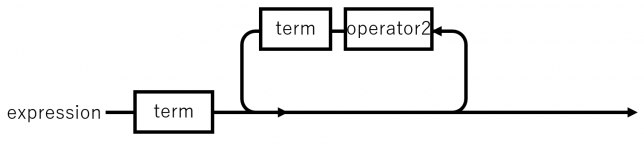
項を分解する
次に項を分解します。
項は掛け算や割り算の連鎖でつながっているまとまりになります。
単に数値どうしの掛け算・割り算ではなく、括弧が付いた塊とも掛け算・割り算をされます。
ここで、掛け算や割り算でつながっている部分は、因数と呼ばれています。
これをBNFで表現してみます。
<term>::=<factor><operator1><factor> | <factor>
ここで、<factor>は因子、<operator1>は掛け算・割り算（剰余計算を含む）です。
レールロード・ダイヤグラムでは次になります。
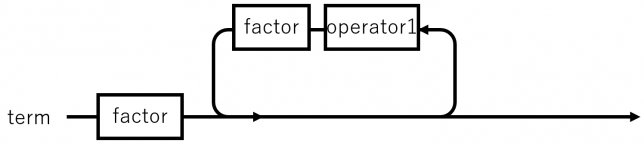
因数を分解する
次に因数を分解してみます。（因数分解をするわけではありません）
因数は、掛け算・割り算でつながっているひとつひとつの数式などです。
因数になり得るものは、数値であるか括弧で囲まれた数式であるかのいずれかになります
これをBNFで表現してみます。
<factor>::=<numeral> | “(" + <expression> “)"
数値<numeral> は、そのまま因子になります。
数値だけではなく、括弧で囲まれた式も因子になり得ます。
このBNFをレールロード・ダイアグラムで表してみます。
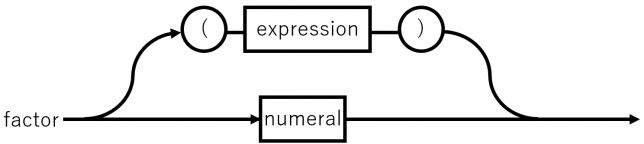
最初の<expression>からたどると、括弧がついている場合には<expression>にが現れます。
間に別のメソッドが現れますが、メソッドを呼び出し続けたときに、再び<expression>が現れ、再帰構造となっています。
そのため、構文解析する際にも再帰的な定義となり、再帰的な処理が行われます。
次回はこれらを解析するプログラムを作っていきます。
今回はこれでおしまいにします。
それではまた。