情報科の目で見る数学科学習指導要領(8)自転車シェアリング

こんにちは。まだまだ数学科との連携できそうな内容について書いていきます。前回は数学Bの中から、漸化式と関連して「ハノイの塔」を取り上げました。数学Bは取り上げていけば、「数列」で書きたいことはいっぱいあるし、その次の「統計的な数列」もいっぱいあります。既に書いた「ベイズの定理」もまだまだ不十分です。全部書いていたら、このシリーズは果てしなくなってしまいそうなので、別の機会に書くことにして、単発として書けるものを対象に進めていきます。そこで今回は「数学B」の「数学と社会生活」で示されている「自転車シェアリング」を取り上げることにします。
「自転車シェアリング」を取り上げた理由
勤務校の授業で、「モデル化とシミュレーション」について生徒に問題を発見させて、それについてのモデル化とシミュレーションをして解決策を探るようなことをしています。
生徒が考えた問題として、「駅に置き傘を置いてほしい。何本あれば足りるかを知ることができれば、解決案が立てられるのではないか」というものがありました。リアルな駅数とリアルな人数を用いたので、結構大変だった記憶がありますが、とても面白い着眼点で、計算も手計算では処理しきれなくコンピュータが有用なものでした。
それは「自転車シェアリング」と同じ考え方を発展させることにより、シミュレーションできます。そのため、手計算するには適度な大きさの「自転車シェアリング」を紹介します。
数学科で例示された「自転車シェアリング」と情報科の関係
学習指導要領解説で、次のような例示があります。
例えば,「自転車シェアリング」に関わる話題として,サイクルポート(専用の貸出・返却場所)の設置台数を考察することが考えられる。「自転車シェアリング」は,都市や観光地での交通渋滞や大気汚染,放置自転車の緩和を目指し,注目を集めている。レンタサイクルと異なるのは,サイクルポートであれば,どこでも自転車を借りたり返したりできることにある。例えば,次のような問題を取り扱い,自転車の設置台数の変化を漸化式を用いて表したり,コンピュータなどの情報機器を用いるなどしてその変化の様子を調べたりすることが考えられる。
設置台数を検討するために,サイクルポートを仮設し社会実験を行った結果,ある日の結果は,次の表のようになった。
| 割合 | |
| A → A | 0.3 |
| A → B | 0.7 |
| B → A | 0.4 |
| B → B | 0.6 |
例えば,A→Aは,Aで借りられた自転車のうちの30%がAで返却されたことを表している。この割合に基づいて,ポートの設置台数について考察する。さらに,この割合が変化するとどうなるか,を考察する。
少し本筋から話は逸れますが、川越市は蔵の街で平日にも結構な観光客が来ています。それもあってか自転車シェアリングが5年前から始まりました。(この記事が公開されるときには、運営主体が変わるため休止中ですが)この自転車を見る度に「自転車が足らなくなったり、置き場が足らなくなって返すのに困ったりしないのかな?」と疑問に思っていました。
上のリンクから説明を読むと、満車時の返却方法が書いてありました。しかし、偏りが生じてきたら、自転車を移動しなければならないはずです。
このようなことを調べるには、数学が役に立つし、さらにコンピュータを使って予測できればさらに有用です。コンピュータを使って予想することは、正に「モデル化とシミュレーション」ですね。
予想してみましょう
実際に計算したり、コンピュータでシミュレーションしたり、などのことをいきなり始めないで予想してみましょう。
それでは、予想する時間を取ります。
・
・
・
・
・
はい、予想できましたか?次に進みましょう。
ちなみに、私の予想は「Aは最初の台数より減り、Bは最初の台数より増えて、最終的には一定の台数に近づく」というものです。
モデル1(自転車の台数の変化に着目したモデル)
自転車の変化を数式で表現してみましょう。ある日の朝の自転車の台数を、Aのサイクルポートには\(x_n\)台、Bのサイクルポートには\(y_n\)台あったとします。この日の夕方の台数がそれぞれ\(x_{n+1}\)台、\(y_{n+1}\)台になったとすると、次のような式で求められます。
\[ \begin{eqnarray} \left\{ \begin{array}{l} x_{n+1} = 0.3 x_n + 0.4 y_n\\ y_{n+1} = 0.7 x_n + 0.6 y_n \end{array} \right. \end{eqnarray}\]
これをモデルとして、自転車の台数の変化が調べることにしましょう。
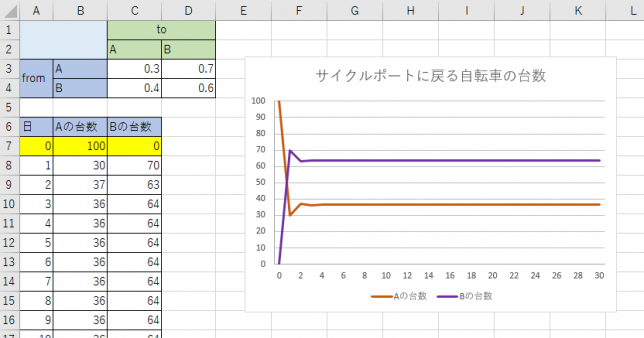
はじめに、Aに100台、Bに0台あるものとして日ごとの台数の変化を見てみます。
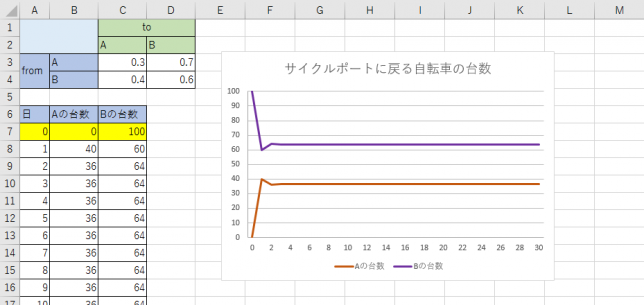
次に、Aに0台、Bに100台あるものとしてシミュレーションしてみます。
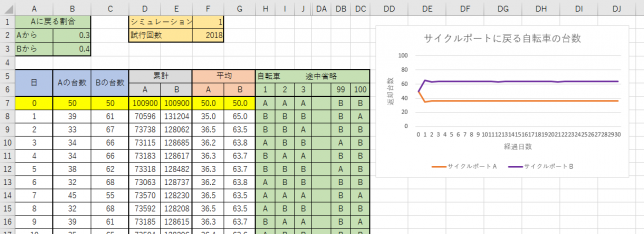
次に、Aに50台、Bに50台あるものとしてシミュレーションしてみます。
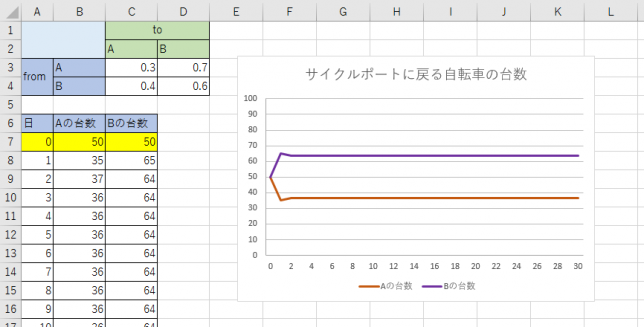
いずれの場合も何日か経過するとAに36台、Bに64台になっていきます。
モデル2(自転車ごとに戻されるサイクルスポットをランダムで決めるモデル)
モデル1は自転車の台数に着目してモデル化を行いました。その結果のシミュレーションは、きれいに収束してしまいリアリティに欠けている感じがします。
そこで、全部で100台の自転車があると仮定したときに、100台すべての自転車に対しランダムでどちらのサイクルスポットに戻されるかを決めてシミュレーションしてみよう!というモデルになります。自転車の台数と同じ100列分使うので、「乱数→元のサイクルスポットに応じた比率→返却されるサイクルスポット」を1つの式でまとめて書くと次のようになります。
=rand()<(元のサイクルスポット→Aに戻される割合)
この式が真ならばサイクルスポットAに、偽ならばサイクルスポットBに返却されます。実際にExcel上では「A」または「B」と表示するために
=CHAR( CODE(“A") + ( RAND() < INDEX(返却割合を示した表,CODE(借りたサイクルスポット)-CODE(“A")+1) ) )
により求めています。Excelでシミュレーションした結果は、次のようになります。
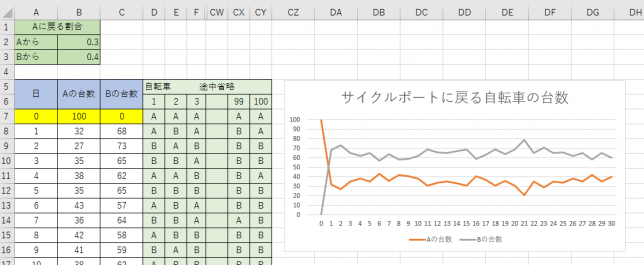
乱数を用いているので振動していますが、モデル1で求めた値に近いあたりになりそうです。確認のため、2018回ほどシミュレーションを繰り返して平均を求めてみました。概ねモデル1の数値に近い値になっています。
数学的に考えると
現在の学習指導要領も次期学習指導要領も、高校の数学科から「行列」はなくなっているのですが、行列を使って表すと
\[\begin{pmatrix} x_{n+1} \\ y_{n+1} \end{pmatrix}=\begin{pmatrix} 0.3 & 0.4 \\ 0.7 & 0.6 \end{pmatrix} \begin{pmatrix} x_n \\ y_n \end{pmatrix}\]
と表せます。
\(n\)日経過したときの自転車の台数を調べるには
\[ \begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix} = \begin{pmatrix} 0.3 & 0.4 \\ 0.7 & 0.6 \end{pmatrix} ^ n \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} \]
により求められます。行列の問題としては、行列を対角化して累乗を求める問題にできます。詳しい説明は端折りますが、次のように求められます。(行列を学習していない人は、行列の固有値・行列の対角化・逆行列について調べてみてください。)
\[ A= \begin{pmatrix} 0.3 & 0.4 \\ 0.7 & 0.6 \end{pmatrix} \]
としたときに、
\[ P= \begin{pmatrix} 1 & 4 \\ -1 & 7 \end{pmatrix} \]
とすると\( P \)の逆行列\( P^{-1} \)は
\[ P^{-1}= \begin{pmatrix} \frac{7}{11} & -\frac{4}{11} \\ \frac{1}{11} & \frac{1}{11} \end{pmatrix} \]
となり、
\[ P^{-1}AP = \begin{pmatrix} -0.1 & 0 \\ 0 & 1 \end{pmatrix} \]
により対角化できます。よって
\[ {(P^{-1}AP)}^n = P^{-1}AP \cdot P^{-1}AP \cdot \ldots \cdot P^{-1}AP = P^{-1}A^n P = \begin{pmatrix} (-0.1)^n & 0 \\ 0 & 1 \end{pmatrix} \]
となることから
\[ A^n = P(P^{-1}A^nP) P^{-1} = \begin{pmatrix} \frac{7(-0.1)^n+4}{11} & \frac{-4(-0.1)^n+4}{11} \\ \frac{-7(-0.1)^n+7}{11} & \frac{4(-0.1)^n+7}{11} \end{pmatrix} \]
と\(A^n\)が求められます。したがって、
\[ \begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix} = \begin{pmatrix} \frac{7(-0.1)^n+4}{11} & \frac{-4(-0.1)^n+4}{11} \\ \frac{-7(-0.1)^n+7}{11} & \frac{4(-0.1)^n+7}{11} \end{pmatrix} \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} = \begin{pmatrix} \frac{7(-0.1)^n+4}{11} x_0 + \frac{-4(-0.1)^n+4}{11} y_0 \\ \frac{-7(-0.1)^n+7}{11} x_0 + \frac{4(-0.1)^n+7}{11} y_0 \end{pmatrix}\]
により\(n\)日後のそれぞれのサイクルスポットの自転車の台数が求められます。ここで、\(n\)がある程度大きい場合、\((-0.1)^n \sim 0 \)であることから
\[ \begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix} \sim \begin{pmatrix} \frac{4(x_0+y_0)}{11} \\ \frac{7(x_0+y_0)}{11} \end{pmatrix}\]
となり、サイクルスポットAとサイクルスポットBに返却される割合は\(4:7\)の比率に収束することが分かります。初期値がどのような値であっても一定の比率に収束するというのは、私にとっては意外な結果でした。
まとめ
自転車の台数の変化の傾向をつかむのであれば、台数の変化に着目したモデルによるシミュレーションをするか、行列を計算すれば予想できます。リアリティを求めるならば、自転車1台ごとにシミュレーションをすることになります。ただし、値が振動してしまうために傾向はわかりにくくなることは否めません。やりたいことによってモデルは変わってくるので、やりたいことに応じて考えていく必要があります。
今回はここまでします。それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません