情報科の目で見る数学科学習指導要領(1)線形計画法

こんにちは。前回まで高等学校の数学科の変遷について、学習指導要領をもとに確認してきました。このように確認してきた理由として、数学科が日常や社会の問題を意識した結果、案外情報科との境界が重なってきたのではないかと感じたことがあります。
新学習指導要領解説を熟読するとそのような記述が多くあります。それらを題材として、何回かに分けて取り上げたいと思います。その第1回として、数学Ⅱの(2)図形と方程式に書かれている線形計画法を取り上げたいと思います。
問題
2つの材料a,bがあり、1日で使用できる量が限られています。これらの材料を組み合わせて2つの製品A,Bを製造します。製品A,Bを販売したときの利益が最大になるようにするには製品A,Bをそれぞれ何個製造したときか。また、その利益を求めよ。(多少ですが、数値を変えています)
| 製品A | 製品B | 使用限度 | |
| 材料a | 1kg | 4kg | 200kg |
| 材料b | 4kg | 2kg | 400kg |
| 1個あたりの利益 | 2000円 | 3000円 |
解法
もちろん数学Ⅱの(2)図形と方程式で取り上げられているので、不等式が表す領域の問題であることは十分承知しています。しかし、情報科の問題として解くのであれば、「モデル化とシミュレーション」しかないでしょう!
その流れで説明していきます。
製品Aをx個作ったと仮定してシミュレーションします。
製品Aをx個作るには
材料aの使用量 = 1kg × x 個
材料bの使用量 = 4kg × x個
ずつ材料を使います。
次に、製品Bを作るために使用できる材料の量(残量)を確認しましょう。
材料aの残量 = 200kg – 材料aの使用量
材料bの残量 = 400kg – 材料bの使用量
となります。表計算ソフトウェアでは、別の列に材料a,bの使用量が計算されているので、数学のように式を整理したりしません。
この残量は製品Bの何個分になっているかを求めましょう。
材料aは何個分 = 材料aの残量 / 4kg
材料bは何個分 = 材料bの残量 / 2kg
材料a,bが揃って製品Bが作れるので、この個数の少ない方が製品Bを作れる個数になるので
製品Bを作れる個数y = int(min(材料a,bは何個分))
です。intを付けたのは、個数は自然数であるためです。
これで、製品A,Bを何個作るかが決まったので
利益 = 2000円 * x + 3000円 * y
により利益が求まります。
表計算ソフトウェアの利用
これに基づいて表計算ソフトウェアに式を入力すると、次のようになります。
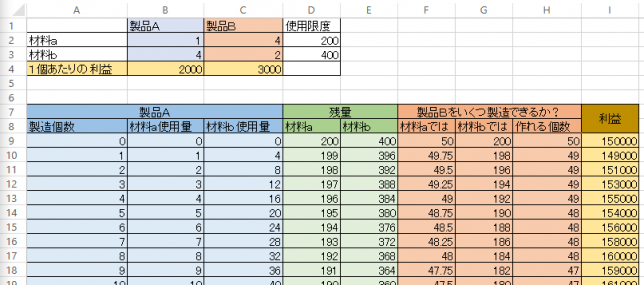
製品Aの個数と利益の関係について折れ線グラフを描くと
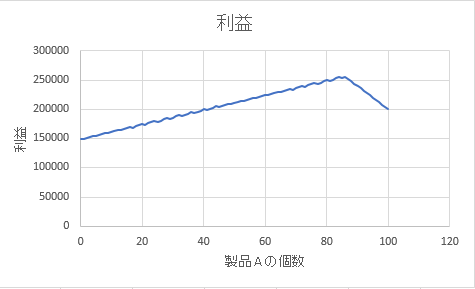
となり、製品Aが80個より少し多いくらいで利益が最大化します。このあたりの表を読み取ると、
製品A 86個
製品B 28個
利益 256,000円
ということがわかります。
不等式が表す領域の問題として考えると
今回は数学科での不等式が表す領域の解法には深く触れませんが、製品Aを製造する個数をx個、製品Bを製造する個数をy個として、材料a,bについて不等式を作り、
G=2000x+3000y
を変形した
y=-2/3x+G/3000
の切片(G/3000)を最大化するようなx,yを見つければ求まります。
それではまた。












ディスカッション
コメント一覧
まだ、コメントがありません